正方形と最短距離の面積比と面積の問題

問題１３図の四角形$ABCD$は正方形である。
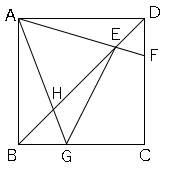
$E$は、線分$DB$上の点で、$DE：EB=1:3$であり、$F$は直線$AE$と辺$DC$との交点である。
また、$G$は辺$BC$上にあり、線分$AG$と$GE$の長さの和が最小となる点で、$H$は線分$AG$と$EB$との交点である。
$AB=8cm$のとき、△$AHE$の面積は何$cm²$ですか。

方針

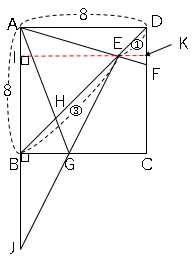
点$E$から垂線を引き、$AB$との交点を$I$とする。
点$E$から垂線を引き、$DC$との交点を$K$とする。
また、点$A$を線分$BC$に対して対称移動させた点を$J$とする。
これで$G$の位置は線分$BC$と線分$JE$との交点となる。

△$BIE$∽△$DKE$なので、
（∠$BIE=$∠$DKE=90°$、∠$IBE=$∠$KDE=45°$で$2$角がそれぞれ等しい）
$IE:KE=BE:ED$
$IE:KE=3:1$
$AD=8$なので、
$IE=8×\displaystyle \frac{3}{4}$
$IE=6$

△$IBE$は$45,45,90°$の特別な三角形なので、$IB=6$
対称移動より、$AB=BJ=8$

△$JBG$∽△$JIE$なので、
（∠$JBG=$∠$JIE=90°$、∠$J$は共通なので$2$角がそれぞれ等しい）
$JB:JI=BG:IE$
$8:8+6=BG:6$
$BG=\displaystyle \frac{48}{14}$
$BG=\displaystyle \frac{24}{7}$

角の$2$等分線より
$AB:BG=AH:HG$
$8:\displaystyle \frac{24}{7}=AH:HG$
$7:3=AH:HG$

△$BHG$∽△$DHA$なので、
（対頂角より∠$BHG=$∠$DHA$、∠$HBG=$∠$HDA=45°$で$2$角がそれぞれ等しい）
$BH:HD=HG:AH$
$BH:HD=3:7$

ここで、図のようにまとめる。


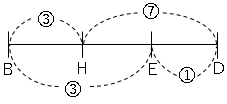
$BH:HD=7:3$
$BE:ED=3:1$

$HD=7a,ED=b$とすると、
$BH=3a,BE=3b$となる。
これより
$3a+7a=b+3b$
$a=\displaystyle \frac{2}{5}b$

ゆえに
$BH:HE:ED=3a:3b-3a:b$
$BH:HE:ED=\displaystyle \frac{6}{5}b:3b-\displaystyle \frac{6}{5}b:b$
$BH:HE:ED=\displaystyle \frac{6}{5}b:\displaystyle \frac{9}{5}b:\displaystyle \frac{5}{5}b$
$BH:HE:ED=6:9:5$

これより△$AHE$は
△$ABD$の$\displaystyle \frac{9}{6+9+5}$倍
よって
△$AHE=\displaystyle \frac{9}{20}×8×8÷2$
△$AHE=\displaystyle \frac{72}{5}$