弧が等しい場合の証明問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
5166 Views
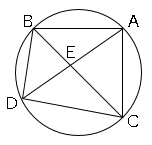
問題１２図のように、$3$点$A,B,C$が円周上にあり、$\stackrel{ \Large \frown }{ AB }=\stackrel{ \Large \frown }{ AC }$です。
また、$A$を含まない$\stackrel{ \Large \frown }{ BC }$上に$B,C$と異なる点$D$をとります。
点$E$は$2$つの線分$AD$と$BC$の交点です。
このとき、$BE:AC=ED:CD$となることを証明しましょう。
また、$A$を含まない$\stackrel{ \Large \frown }{ BC }$上に$B,C$と異なる点$D$をとります。
点$E$は$2$つの線分$AD$と$BC$の交点です。
このとき、$BE:AC=ED:CD$となることを証明しましょう。
方針
$BE:AC=ED:CD$を証明するのだから、これらを含む三角形を探して証明する。
証明する三角形を見つける。
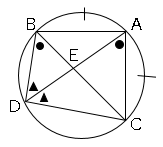
△$BDE$と△$ADC$において
$\stackrel{ \Large \frown }{ AB }=\stackrel{ \Large \frown }{ AC }$であり、
等しい弧に対する円周角は等しいので、
∠$BDE=$∠$ADC$・・・➀
また、$\stackrel{ \Large \frown }{ DC }$に対する円周角は等しいので、
∠$DBE=$∠$DAC$・・・➁
➀、➁より$2$角がそれぞれ等しいので、
△$BDE$∽△$ADC$
よって対応する辺の比はそれぞれ等しいので、
$BE:AC=ED:CD$
不明点があればコメント欄よりお願いします。