直角二等辺三角形と面積の問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
4456 Views
問題１４図のように、$AB=AC$、∠$BAC=90°$の直角二等辺三角形$ABC$と$DB=DE$、∠$BDE=90°$の直角二等辺三角形$DBE$がある。
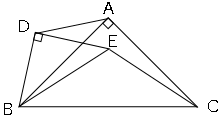
（１）△$ADB$∽△$CEB$を証明しましょう。
（２）$AB=3cm$、$DB=2cm$とし、$3$点$D,E,C$がこの順に一直線上に並ぶとき、△$ADB$の面積を求めましょう。
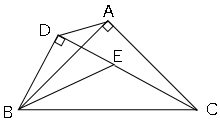
（１）△$ADB$∽△$CEB$を証明しましょう。
（２）$AB=3cm$、$DB=2cm$とし、$3$点$D,E,C$がこの順に一直線上に並ぶとき、△$ADB$の面積を求めましょう。
方針
（１）を使って（２）を求める。
角と辺の情報は同じくらいだから、相似の条件も両方を満たすだろうと考える。
（１）
△$ADB$と△$CEB$において、
△$DBE$は直角二等辺三角形なので、$DB：BE=1:\sqrt{2}$・・・➀
△$ABC$は直角二等辺三角形なので、$AB：BC=1:\sqrt{2}$・・・➁
➀、➁より$AB:CB=DB:EB=1:\sqrt{2}$・・・➂
∠$ABD=$∠$DBE-$∠$ABE=45-$∠$ABE$・・・➃
∠$EBC=$∠$ABC-$∠$ABE=45-$∠$ABE$・・・➄
➃、➄より∠$ABD=$∠$EBC$・・・➅
➂、➅より
$2$辺の比とその間の角がそれぞれ等しいので、
△$ADB$∽△$CEB$
（１）を利用して（２）を求める。
（２）
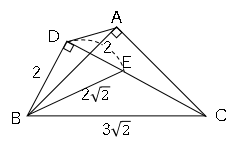
△$ADB$∽△$CEB$なので
面積比は相似比の$2$乗なので、
△$ADB:$△$CEB$
$DB²:EB²$
$=2²:(2\sqrt{2})²$
$=1:2$
△$CEB$の面積は$CE×DB÷2$なので$CE$の長さを求める。
三平方の定理より
$DC²=BC²-DB²$
$DC²=18-4$
$DC=\sqrt{14}$
これより
$CE=\sqrt{14}-2$
△$CEB$の面積は
$CE×DB÷2$
$=(\sqrt{14}-2)×2÷2$
$=\sqrt{14}-2$
△$ADB:$△$CEB=1:2$なので
△$ADB$の面積は$\displaystyle \frac{\sqrt{14}-2}{2}$
不明点があればコメント欄よりお願いします。