規則性とマス目の問題

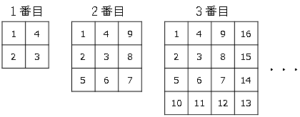
問題８図のように、連続する自然数をある規則に従って、$1$番目、$2$番目、$3$番目、・・・と並べていく。
このとき、$3$番目の右上すみにある自然数は$16$、左下隅にある自然数は$10$となっている。
（１）$4$番目の右上すみにある自然数を答えましょう。
（２）$n$番目の右上すみにある自然数$n$を用いて表しましょう
（３）右上すみにある自然数と左下すみにある自然数の和が$146$となるのは何番目ですか。

方針

$1$番目の右すみは$4=2×2$
$2$番目の右すみは$9=3×3$
$3$番目の右すみは$16=4×4$
・・・
$n$番目の右すみは$(n+1)²=(n+1)×(n+1)$
となる。

（１）
$4$番目の右すみは
$5×5$
$=25$

（２）
$n$番目の右すみは$(n+1)²$

（３）
右上すみは（２）より$(n+1)²$
左下すみは$1$個前の右上すみに$1$を足したものになる。
これより、
$(n+1)²+n²+1=146$
$n²+2n+1+n²+1=146$
$2n²+2n=144$
$n²+n-72=$
$(n+9)(n-8)=0$
$n=-9,8$
これより$8$番目