【面積】円の面積の変わった求め方の問題

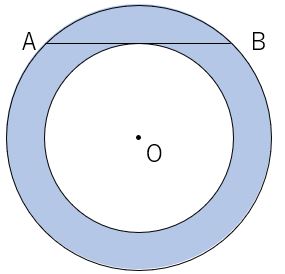
問題１９図は点$O$を中心とする大きい円と小さい円で、大きい円の弦$AB$は小さい円と接している。
$AB=8cm$のとき、青色の部分の面積を求めましょう。ただし円周率は$π$とする。

方針

以下の図のように点を置き補助線を引く。
点$CO$の長さを$x$とおく。
すると∠$ACO$は$90°$となる。
※接線と中心を結んだ角度は$90°$になるから

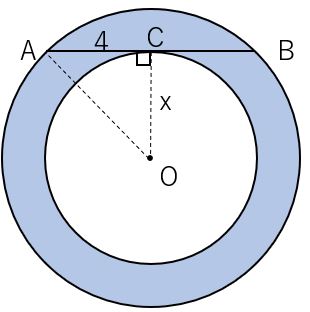
そして△$ACO$に三平方の定理を用いて、
$AO²＝AC²+CO²$
$AO²＝4²+x²$
$AO＝\sqrt{16+x²}$

すると大きい円の面積は、
$\sqrt{16+x²}×\sqrt{16+x²}×π$
$=(16+x²)π$

小さい円の面積は
$x×x×π$
$=x²π$

大きい円の面積から小さい円の面積を引くと、うまく$x$が消える。
$(16+x²)π-x²π$
$=16π$