弧の特徴を利用した相似の証明問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
4928 Views
問題２図の円において、弧AB=弧BC=弧CDで、線分BEと線分ADの交点をFとするとき、△ACE∽△FDEを証明しなさい。
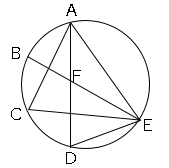
方針
辺と角の情報でどちらが多いか考える。この場合は角の方が多いから角に関する相似の条件を考える。
図の中に情報を書き込む
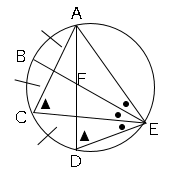
円周角の定理より、∠ACE＝∠ADE
弧AB=弧BC=弧CDなので、∠AEB＝∠BEC＝∠CED
証明
△ACEと△FDEにおいて、
円周角の定理より、∠ACE＝∠ADE・・・➀
∠AEC
＝∠AEB＋∠BEC
(弧AB=弧BC=弧CDなので、∠AEB＝∠BEC＝∠CED)
＝∠BEC＋∠CED
＝∠FED・・・➁
➀、➁より2角がそれぞれ等しいので、
△ACE∽△FDE
不明点があればコメント欄よりお願いします。