タイルの枚数と計算の工夫の問題

問題１９図のように、同じ大きさの正三角形の白いタイルと黒いタイルをすきまなくしきつめて、１番目、２番目、３番目、４番目、・・・$n$番目まで正三角形を作る。

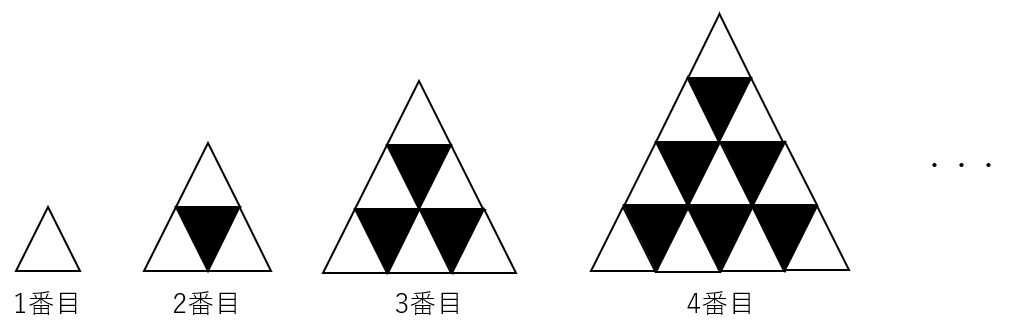
$n$番目の正三角形をつくるのに必要な黒いタイルの枚数を$a$とすると、$a$を$n$を使った式で表しなさい。

方針

$1$番目の白の枚数は$1=(1)$枚
$2$番目の白の枚数は$3=(1+2)$枚
$3$番目の白の枚数は$6=(1+2+3)$枚
$4$番目の白の枚数は$10=(1+2+3+4)$枚
・・・
ｎ番目の白の枚数は$\displaystyle \frac{n(n+1)}{2}=(1+2+・・・+n-1+n)$

※４番目の白の枚数は
$(1+2+3+4=(1+4)+(2+3)=5×2=10)$
足して$5$となるペアが$2$個あるので$10$。
これを$n$番目で試してみると
最初と最後を足すと$(1+n)$でそのペアは全体の半分になるから、$\displaystyle \frac{n}{2}$個
これをかけて$\displaystyle \frac{n(n+1)}{2}$

全体の枚数は
$1$番目の枚数は$1=(1²)$枚
$2$番目の枚数は$4=(2²)$枚
$3$番目の枚数は$9=(3²)$枚
$4$番目の枚数は$16=(4²)$枚
・・・
$n$番目の枚数は枚$n²$

これより黒のタイルの枚数は全体から白のタイルの枚数を引けばよいので、
$a=n²-\displaystyle \frac{n(n+1)}{2}$
$a=\displaystyle \frac{n²-n}{2}$