円周角の定理と作図
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
13798 Views
問題１０
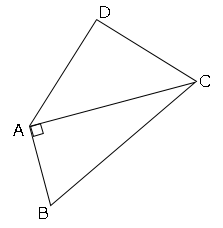
図のように四角形ＡＢＣＤがあり、対角線ＡＣを引く。∠ＢＡＣ＝９０°とする。
辺ＣＤ上に、∠ＡＣＢ＝∠ＡＰＢとなる点Ｐを作図せよ。
図のように四角形ＡＢＣＤがあり、対角線ＡＣを引く。∠ＢＡＣ＝９０°とする。
辺ＣＤ上に、∠ＡＣＢ＝∠ＡＰＢとなる点Ｐを作図せよ。
方針最終的に求める点を作図してから、何をすればいいか考える。
まず点Ｐを作図する。
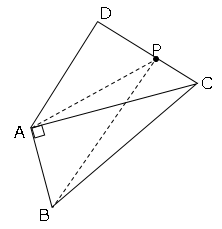
∠ＢＡＣ＝９０°なので、ＢＣを直径とする円を描く。
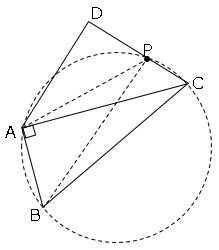
ここで円周角の定理の性質を使う。
∠ＡＣＢ＝∠ＡＰＢとなる。
まず点Ｐを作図する。
∠ＢＡＣ＝９０°なので、ＢＣを直径とする円を描く。
ここで円周角の定理の性質を使う。
∠ＡＣＢ＝∠ＡＰＢとなる。
➀ＢＣの垂直二等分線で円の中点を求める。
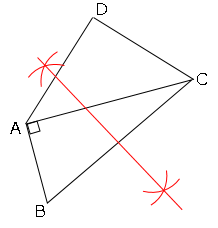
➁➀で求めた中点と点Ｂの長さを半径とする円を描く。
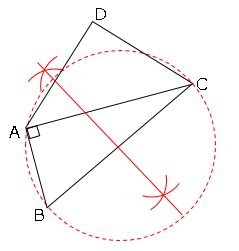
➂作成した円とＤＣの交点がＰとなる。
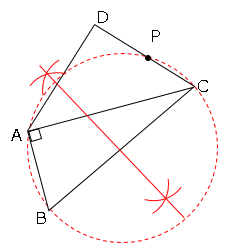
不明点があればコメント欄よりお願いします。