直角三角形と円周角の定理を利用した合同の証明問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
7512 Views
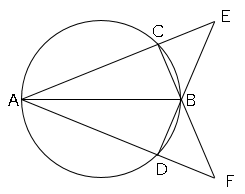
問題５図のように、線分ＡＢを直径とする円の周上に、２点Ｃ，Ｄを∠ＢＡＣ＝∠ＢＡＤとなるようにとる。ただし、ＡＣ＞ＢＣとする。また、直線ＡＣと直線ＤＢとの交点をＥ、直線ＡＤと直線ＣＢとの交点をＦとする。このとき、ＢＥ＝ＢＦとなることを証明しなさい。
方針
辺と角の情報でどちらが多いか考える。この場合は円があるから角の方が多いから角に関する相似・合同の条件を考える。
ＢＥ＝ＢＦなので、△ＣＢＥと△ＤＢＦを示す。そのためにまずは△ＡＢＣと△ＡＢＤを示す。
△ＡＢＣと△ＡＢＤにおいて、
仮定より、∠ＢＡＣ＝∠ＢＡＤ・・・①
線分ＡＢは直径なので円周角の定理より、
∠ＡＣＢ＝∠ＡＤＢ・・・②
またＡＢは共通・・・③
➀、②、③より
斜辺と１つの鋭角がそれぞれ等しいので、
△ＡＢＣ≡△ＡＢＤ・・・④
また△ＣＢＥと△ＤＢＦについて
∠ＢＣＥ＝∠ＢＤＦ＝９０°・・・⑤
対頂角より、∠ＣＢＥ＝∠ＤＢＦ・・・⑥
④よりＢＣ＝ＢＤ・・・⑦
⑤、⑥、⑦より
１辺とその両端の角がそれぞれ等しいので
△ＣＢＥ≡△ＤＢＦ
対応する辺はそれぞれ等しいので、
ＢＥ＝ＢＦ
不明点があればコメント欄よりお願いします。