平行四辺形の性質を利用した辺の長さを求める問題

問題４図のように、ＡＢ＝１０ｃｍの平行四辺形ＡＢＣＤがあります。
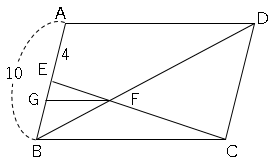
辺ＡＢ上に、ＡＥ＝４ｃｍとなる点Ｅをとり、線分ＥＣをひきます。
線分ＥＣと対角線ＢＤとの交点をＦとし、点Ｆを通って辺ＢＣに平行な直線と辺ＡＢとの交点をＧとします。
このとき、線分ＥＧの長さを求めなさい。

方針

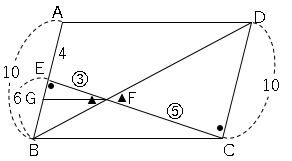
△$EBF$∽△$CDF$なので
$EF:FC=EB:DC$
$EF:FC=6:10=3:5$

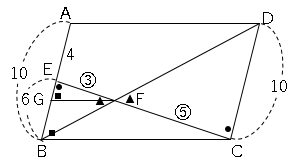
△$EGF$∽△$EBC$なので
$EG:EB=EF:EC$
$EG:6=3:8$
$EG=\displaystyle \frac{9}{4}$