折り目を利用した相似の証明問題と線分の長さ
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
9968 Views
問題6図のように、長方形ABCDで、対角線BDを折り目として△BCDを折り返したところ、頂点Cが点Eに移った。辺ADと線分BEとの交点をFとする。また、AGは頂点AからBDに引いた垂線であり、BEとAGとの交点をHとする。
(1)△ABG∽△BDEを証明せよ。
(2)AB=3cm、BC=4cmのとき、BG、AHの長さを求めなさい。
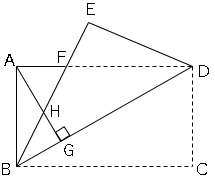
(1)△ABG∽△BDEを証明せよ。
(2)AB=3cm、BC=4cmのとき、BG、AHの長さを求めなさい。

方針
辺と角の情報でどちらが多いか考える。この場合は折り目があるから角の方が多いから角に関する相似・合同の条件を考える。線分の長さは証明を使うことが多い。
(1)折り目に注目して考える
△ABGと△BDEにおいて、
長方形の折り目より、∠BCD=∠BED=90°・・・➀
また、垂線より∠AGB=90°・・・➁
➀、➁より∠AGB=BED・・・➂
長方形の錯角より、∠ABG=∠CDB・・・➃
また折り目より、∠BDE=∠CDB・・・⑤
➃、⑤より∠ABG=∠BDE・・・➅
➂、➅より2角がそれぞれ等しいので
△ABG∽△BDE
(2)わかる長さを図に書きこむ
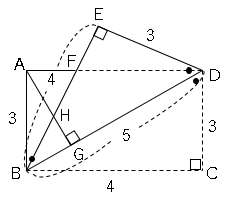
直角三角形BDE特別な三角形なのでBD=5
(1)より△ABG∽△BDEなので、
$AB:BG=BD:DE$
$3:BG=5:3$
$BG=\displaystyle \frac{9}{5}$
BGの長さを使って出すことを考える。数学が基本前の解答を使うから
AGの長さは△ABG∽△BDEなので、
$AG:AB=BE:BD$
$AG:3=4:5$
$AG=\displaystyle \frac{12}{5}$
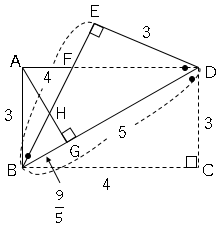
図より△BGH∽△BEDより
$BG:GH=BE:ED$
$\displaystyle \frac{9}{5}:GH=4:3$
$GH=\displaystyle \frac{27}{20}$
これよりAHの長さは
$AH=AG-HG$
$AH=\displaystyle \frac{12}{5}-\displaystyle \frac{27}{20}$
$AH=\displaystyle \frac{21}{20}$
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません