正三角形と円周角の定理を用いた合同・相似の証明問題

問題８図のように、円Ｏの円周上にある３点Ａ、Ｂ、Ｃを頂点をする正三角形ＡＢＣがある。
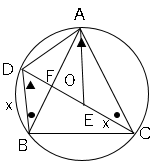
点Ｃを含まない弧ＡＢ上に、２点Ａ、Ｂとは異なる点Ｄをとり、点Ｄと３点Ａ、Ｂ、Ｃをそれぞれ結ぶ。
線分ＣＤ上に、ＢＤ＝ＣＥとなる点Ｅをとり、点Ａと点Ｅを結ぶ。

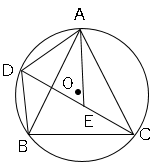
（１）△ＡＢＤ≡△ＡＣＥを証明せよ。
（２）△ＡＤＥが正三角形であることを証明せよ。
（３）ＡＤ＝２ｃｍ、ＢＣ＝３ｃｍのとき、線分ＣＥの長さを求めなさい。

方針

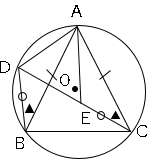
△ＡＢＤと△ＡＣＥにおいて、
仮定よりＢＤ＝ＣＥ・・・➀
円周角の定理より∠ＡＢＤ＝∠ＡＣＥ・・・➁
正三角形ＡＢＣよりＡＢ＝ＡＣ・・・➂
➀、➁、➂より
２辺とその間の角がそれぞれ等しいので、
△ＡＢＤ≡△ＡＣＥ

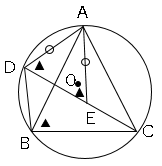
（１）よりＡＤ＝ＡＥなので△ＡＤＥは二等辺三角形になる。
∠ＡＢＣ＝６０°で円周角の定理より、∠ＡＢＣ＝∠ＡＤＣ＝６０°
△ＡＤＥは二等辺三角形なので、∠ＡＥＤ＝６０°
よって∠ＤＡＥ＝６０°
これより△ＡＤＥは正三角形となる。

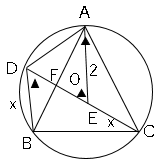
$EC$の長さを$x$とすると、（１）$DB$の長さも$x$となる。
図のように点$F$をおき、$FD=a$すると、
△ＤＢＦ∽△ＥＡＦ（２角が等しい）
$DB:EA=FD:FE$
$x:2=a:2-a$
$2a=x(2-a)$
$2a+ax=2x$
$a=\displaystyle \frac{2x}{2+x}$

これよりＦＥの長さは
$FE=2-FD$
$FE=2-\displaystyle \frac{2x}{2+x}$
$FE=\displaystyle \frac{4}{2+x}$

同様に$BF=b$とすると、
$DB:EA=BF:AF$
$x:2=b:3-b$
$2b=x(3-b)$
$2b+bx=3x$
$b=\displaystyle \frac{3x}{2+x}$

△ＤＢＦ∽△ＡＣＦ（２角が等しい）
$DB:BF=AC:CF$
$x:\displaystyle \frac{3x}{2+x}=3:x+\displaystyle \frac{4}{2+x}$
$x:\displaystyle \frac{3x}{2+x}=3:\displaystyle \frac{2x+x²+4}{2+x}$
$9=2x+x²+4$
$x=-1+\sqrt{6}$（解の公式）