オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
4439 Views
2018年3月17日1次関数中学2年生
問1
グラフは弟が$8$時に家を出発し、歩いて$A$町まで行き、$A$町から自転車で$B$町に行った時のようすを表したものである。家から$A$町まで、$A$町から$B$までのようすを表す直線の式を求めなさい。
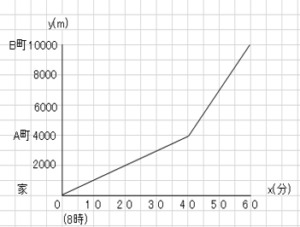
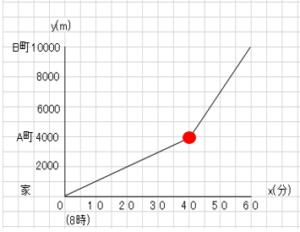
家からA町までは赤点までとなる。原点を通るので、比例の式だとわかる。
$y=ax$の式に$x=40,y=4000$を代入して、
$4000=40a$
$a=100$
$y=100x$となる。
$A$町から$B$町までは、$(40,4000)$と$(60,10000)$の2点を通るので、一次関数だとわかる。
よって$y=ax+b$にそれぞれ代入して、
$\begin{eqnarray}
\left\{\begin{array}{l}40a+b=4000・・・➀\\60a+b=10000・・・➁\end{array}\right.
\end{eqnarray}$
➀$-$➁より
$40a-60a=4000-10000$
$-20a=-6000$
$a=300$・・・➂
➂を➀に代入して、
$12000+b=4000$
$b=-8000$
よって
$y=300x-8000$となる。
問2
図のような長方形$ABCD$の周上を点$P$は毎秒$1cm$の速さで$A$→$B$→$C$→$D$と移動する。$AB=3cm$、$AD=8cm$、点$P$が$A$を出発してから$x$秒後の△$APD$の面積を$ycm²$とする。それぞれの変域に対して$y$を$x$の式で表しましょう。
(1)$0≦x≦3$
(2)$3≦x≦11$
(3)$11≦x≦14$
(4)(1)~(3)のグラフを書きましょう。

動点の問題はそれぞれの変域の図をかくとわかりやすい。
毎秒$1cm$なので、$x$秒後は$xcm$となる。
(1)$0≦x≦3$のとき点$P$は図のような位置にある。
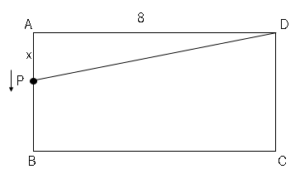
よって△$APD$の面積は
$y=x×8÷2$
$y=4x$
(2)$3≦x≦11$のとき点$P$は図のような位置にある。
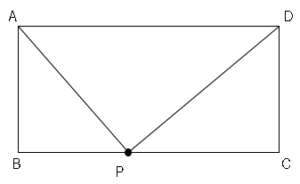
よって△$APD$の面積は底辺と高さが一定なので、
$y=3×8÷2$
$y=12$
(3)$11≦x≦14$のとき点$P$は図のような位置にある。
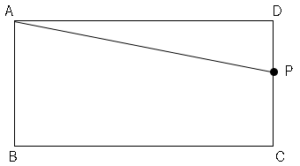
よって△$APD$の面積は
$y=(14-x)×8÷2$
$y=-4x+56$
(4)
$0≦x≦3$のとき、$y=4x$
$3≦x≦11$のとき、$y=12$
$11≦x≦14$のとき、$y=-4x+56$
なので図のようなグラフができる。
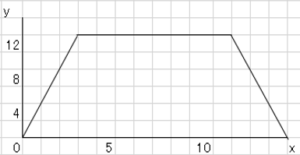

問3
図で、直線$y=2x-2$と直線$y=-2x+6$があり、交点を$A$とする。2直線と$y$軸との交点を$B,C$とする。このとき△$ABC$の面積を求めましょう。
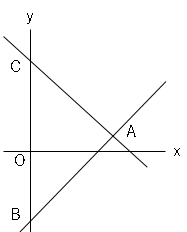
すべての点の座標を求める。
点$A$は交点なので、
$2x-2=-2x+6$
$4x=8$
$x=2$
これより$y=2$
$A(2,2)$
点$B,C$は$y$軸との交点なので、$x$座標はともに$0$となる。
$B(0,-2)$、$C(0,6)$
これより△$ABC$の面積は
$8×2÷2=$
$8$
※底辺は$BC$の長さより$6+2=8$、高さは点$A$の$x$座標なので$2$

問4
2直線$ax+by=8$、$bx+ay=7$が点$(2,3)$で交わるとき、$a,b$の値を求めましょう。
2直線が点$(2,3)$で交わっているので、
$2a+3b=8$、$2b+3a=7$
$\begin{eqnarray}
\left\{\begin{array}{l}2a+3b=8・・・➀\\2b+3a=7・・・➁\end{array}\right.
\end{eqnarray}$
➀×3$-$➁×2より
$9b-4b=24-14$
$b=2$
$b=2$・・・➂
➂を➀に代入して、
$2a+6=8$
$a=1$
問5
直線$ax+y=2$が2直線$2x-y=5$,$x+2y=10$の交点を通るとき、$a$の値を求めましょう。
2直線の交点を求め、$ax+y=2$の式に代入する。
$2x-y=5$
$y=2x-5$を$x+2y=10$に代入して、
$x+4x-10=10$
$5x=20$
$x=4$
よって$y=3$
$ax+y=2$に代入して、
$4a+3=2$
$a=-\displaystyle \frac{1}{4}$

不明点があればコメントよりどうぞ。


















ディスカッション
コメント一覧
まだ、コメントがありません