一次関数の練習問題１
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
6660 Views
2018年3月17日１次関数中学２年生
問１
$y$は一次関数でそのグラフが点$(2,1)$を通り、傾き$2$の直線であるとき、この一次関数を求めましょう。
一次関数は$y=ax+b$と表せる。傾きが$2$なので$y=2x+b$となる。
また点$(2,1)$を通るので、
$y=2x+b$
$1=2×2+b$
$1=4+b$
$b=-3$
よってこの一次関数は
$y=2x-3$
問２
$y$は$x$の一次関数で、２点$(2,3)$,$(-2,-1)$を通る直線であるとき、この一次関数を求めましょう。
一次関数は$y=ax+b$と表せる。２点$(2,3)$,$(-2,-1)$を通るので、
$2a+b=3$、$-2a+b=-1$と表せる。
$a,b$を求めるために連立方程式を解く。
$\begin{eqnarray}
\left\{\begin{array}{l}2a+b=3・・・➀\\-2a+b=-1・・・➁\end{array}\right.
\end{eqnarray}$
➀＋➁より
$b+b=3-1$
$b=1$・・・➂
➂を➀に代入して、
$2a+1=3$
$a=1$
これより、一次関数は$y=x+1$
問３
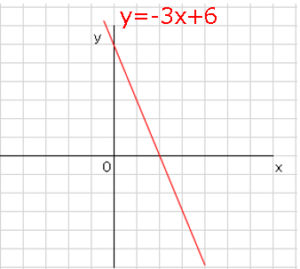
方程式$6x+2y=12$のグラフを書きなさい。
$6x+2y=12$の式を変形して$y=$の形にする。
$3x+y=6$
$y=-3x+6$
あとはこれをグラフにする。
問４
連立方程式
$\begin{eqnarray}
\left\{\begin{array}{l}x+y=4・・・➀\\2x-y=-1・・・➁\end{array}\right.
\end{eqnarray}$
の解をグラフを用いて求めましょう。
➀を変形して
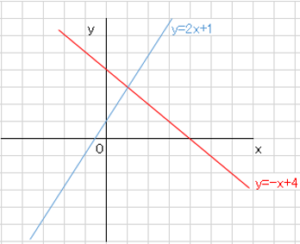
$y=-x+4$、
➁を変形して
$y=2x+1$
これをグラフにして交点を求めると
$(1,3)$
問５
２点$(4,0)$,$(0,2)$を通る一次関数の式を求めましょう。
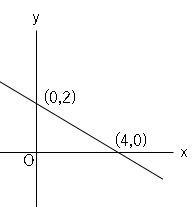
$(0,2)$から切片が$2$であることがわかるので、一次関数の式に代入して、
$y=ax+2$
これが$(4,0)$を通るので、
$0=4a+2$
$a=-\displaystyle \frac{1}{2}$
求める式は$y=-\displaystyle \frac{1}{2}x+2$
不明点があればコメントよりどうぞ。