オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
3697 Views
2018年3月17日1次関数中学2年生
問1
図の直線$m,n$の式は、$m:y=2x+6$,$n:y=\displaystyle \frac{1}{2}x-3$である。
(1)直線$m,n$と$y$軸との交点をそれぞれ$B,C$とする。△$ABC$の面積を求めましょう。
(2)直線$m$上で、点$A,B$の間に点$D$をとる。△$ADC$の面積が$18$になる点$D$の座標を求めましょう。
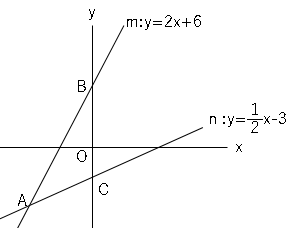

(1)それぞれの点を出し、面積を求める。
点$A$は2直線$m,n$の交点なので、
$2x+6=\displaystyle \frac{1}{2}x-3$
$4x+12=x-6$
$3x=-18$
$x=-6$
よって、$y=-6$
点$A(-6,-6)$
点$B$は直線$m$と$y$軸との交点なので、切片である。点$B(0,6)$
点$C$は直線$n$と$y$軸との交点なので、切片である。点$C(0,-3)$
これを図に書きこんで、整理する。
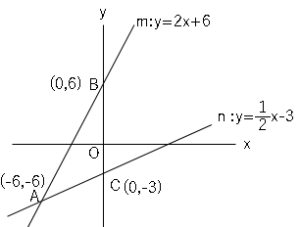
これより△$ABC$の面積は
$9×6÷2=$
$27$
※底辺は$BC=6+3$、高さは点$A$の$x$座標で$6$
(2)
点Dの位置は図のようになる。
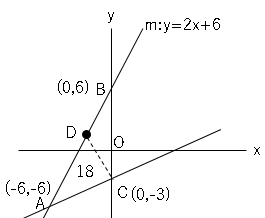
△$ABC$の面積が$27$で△$ADC$の面積が$18$なので、△$DBC$の面積は$9$となる。
△$DBC$の高さを$x$とすると、
$9=9×x÷2$
$x=2$
これより、点$D$の$x$座標は$-2$
ゆえに$m:y=2x+6$に代入して、
$y=2$
点$D$の座標は
$(-2,2)$
問2
3点$(m,2)(-6,6)(0,3)$は一直線上にある。場合の$m$の値を求めましょう。
直線の式を求めて、$(m,2)$を代入する。
2点$(-6,6)(0,3)$の直線の式は$y=ax+b$の式に代入して・・・でもいいが、$(0,3)$を通るので切片が$3$だとわかる。
$y=ax+3$の式に$(-6,6)$を代入する。
$6=-6a+3$
$a=-\displaystyle \frac{1}{2}$
直線の式は$y=-\displaystyle \frac{1}{2}x+3$
これに$(m,2)$を代入して、
$2=-\displaystyle \frac{m}{2}+3$
$4=-m+6$
$m=2$
問3
2直線$x-y=1$、$mx+2y=6$のグラフが交わらないとき、$m$の値を求めましょう。
交わらない=平行=傾きが等しい。
それぞれ$y=$の形に直して、
$y=x-1$、$y=-\displaystyle \frac{m}{2}x+3$
$1=-\displaystyle \frac{m}{2}$
$m=-2$
問4
2点$A,B$の座標はそれぞれ$(-4,2)(8,8)$である。また、点$C$は線分$AB$と$y$軸との交点である。
(1)△$AOB$の面積を求めましょう。
(2)点$C$を通り、△$AOB$の面積を二等分する直線と線分$OB$との交点の座標を求めましょう。
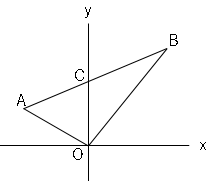
(1)△$AOB$の面積は点$C$を求めて、△$AOC+$△$COB$で求める。
直線$AB$を求めるために$y=ax+b$に代入して
$\begin{eqnarray}
\left\{\begin{array}{l}-4a+b=2・・・➀\\8a+b=8・・・➁\end{array}\right.
\end{eqnarray}$
➀$-$➁より、
$-4a-8a=2-8$
$-12a=-6$
$a=\displaystyle \frac{1}{2}$
よって$b=4$
直線$AB$の式は$y=\displaystyle \frac{1}{2}x+4$
これより点$C$の座標は$(0,4)$
△$AOC$の面積$=4×4÷2=8$
△$COB$の面積$=4×8÷2=16$
△$AOB$の面積は
$24$
(2)図にかきこんでみる。
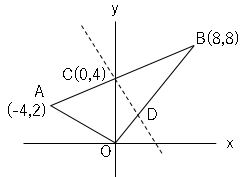
点$D$を求める交点とする。
すると四角形$AODC$の面積は$24÷2=12$となる。
また、四角形$AODC$の面積は△$AOC+$△$COD$なので、
(1)より△$AOC=8$。
△$COD$の高さを$x$とすると、
△$COD=4×x÷2=2x$
よって
$12=8+2x$
$x=2$
ゆえに、点$D$の$x$座標は$2$となる。
(直線$OB$の式は原点を通り比例の式より、$y=ax$。$(8,8)$を代入して$y=x$)
これより点$D$の$y$座標は$2$
求める点は
$(2,2)$

不明点があればコメントよりどうぞ。



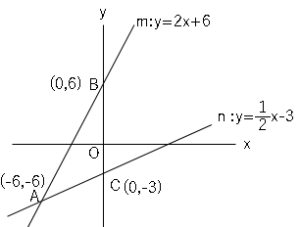









ディスカッション
コメント一覧
まだ、コメントがありません