相似な図形の面積比と表面積と体積の関係
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
11751 Views
相似な図形と面積比
相似な2つの図形で、相似比がa:bならば面積比はa²:b²となります。
注意:相似な図形である場合に限ります。
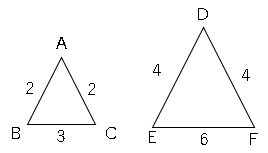
この場合は辺の比がAB:DE=AC:DF=BC:EF=1:2、
△ABC∽△DEFとなり、相似比は1:2なので面積比は1:4
更にここで△ABCの面積を3cm²とすると、△DEFは3×4=12cm²になります。

意味を理解したら問題を解いてみましょう。
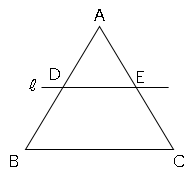
図のように、△ABCの辺BCに平行な直線ℓが、辺ABと点Dで、辺ACと点Eで交わり、AD:DB=2:1です。△ABCの面積が72cm²のとき、△ADEと台形DECBの面積を求めなさい。
相似比と表面積と体積の関係
相似な図形が2つあり、相似比がa:bならば、表面積比はa²:b²、体積比はa³:b³になります。
注意:相似な図形である場合に限ります。
では問題です。図のように三角錐O-ABCの底面ABCに平行な平面Lが、辺OAと点Dで交わり、OD:DA=2:1である。このとき、平面Lで分けられた三角錐の2つの部分P,Qについて、次の問いに答えなさい。
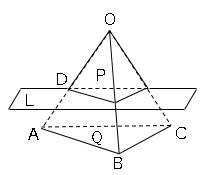

(1)三角錐Pともとの三角錐の表面積の比を求めなさい。
(2)三角錐Pと立体Qの体積比を求めなさい。
(3)三角錐Pの体積が48cm³のとき、立体Qの体積を求めなさい。








ディスカッション
コメント一覧
まだ、コメントがありません