平行線と線分の比と中点連結定理
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
平行線と線分の比
$PQ$//$BC$ならば、△$APQ$∽△$ABC$となるので、$AP：AB=AQ：AC=PQ：BC$となる。
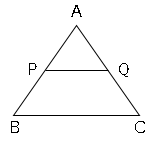
注：これは覚える必要はありません。
簡単に証明できるからです。図に書きこむとわかりますよ。
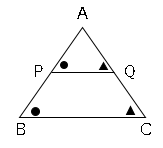
△$APQ$と△$ABC$において、
$PQ$//$BC$なので同位角が等しくなる。
よって∠$APQ=$∠$ABC$・・・➀
また、∠$AQP=$∠$ACB$・・・➁
➀、➁より２角がそれぞれ等しいので、△$APQ$∽△$ABC$
対応する線分の比はそれぞれ等しいので、
$AP：AB=AQ：AC=PQ：BC$
意味を理解したら問題を解いてみましょう。
図で$PQ$//$BC$のとき$x,y$の値をそれぞれ求めなさい。
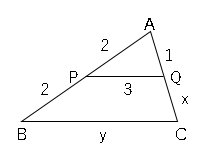
平行線に囲まれた線分の比
２つの直線が３つの平行な直線を図のように交わっているとき、$AB：AC＝DE：DF$
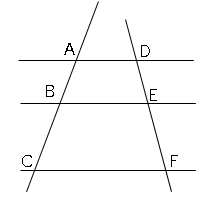
この場合に覚えることは直線を平行に動かすこと。
図のように動かして$AB：AC=DE：DF$を確認しましょう。
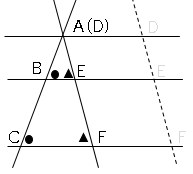
すると△$ABE$∽△$ACF$なので、$AB：AC=DE：DF$となる。
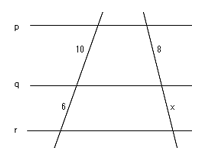
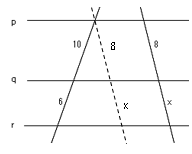
では問題です。図で$p,q,r$が平行のとき$x$の値を求めよ。
中点連結定理
△$ABC$の２辺$AB$、$AC$の中点を、それぞれ$M,N$とすると、
$MN$//$BC,BC=2MN$
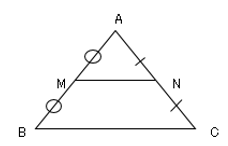
簡単に証明してみましょう。
△$AMN$と△$ABC$において
$AM:AB=1:2$･･･①
$AN:AC=1:2$･･･②
∠$A$は共通・・・③
➀、②、③より
２組の辺の比とその間の角がそれぞれ等しいので、 △$AMN$∽△$ABC$
よって∠$AMN=$∠$ABC$なので
$MN$//$BC$（同位角は等しい）
$AM:AB=MN:BC$
$1:2=MN:BC$
$BC=2MN$
では問題です。△$ABC$で、点$D,E,F$はそれぞれ辺$AB,BC,CA$の中点です。△$DEF$の周りの長さを求めましょう。但し、$AB=6cm､BC=8cm､CA=10cm$とします。
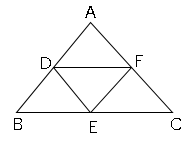
角の２等分線と線分の比
△$ABC$の∠$A$の$2$等分線と辺$BC$との交点を$D$とすると、$AB:AC=BD:DC$となる。
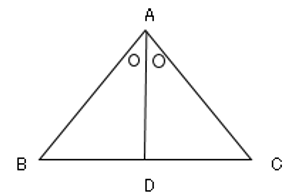
この証明は少し難しいです。補助線の引き方を覚えてしまってかまいません。たまに受験問題で証明の問題が出ます。
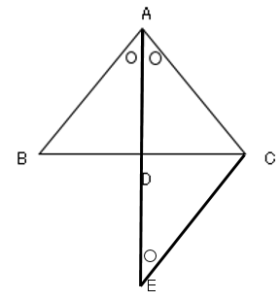
図のように点$C$を通り、$AB$に平行な直線と、直線$AD$の交点を$E$とします。
このとき、∠$BAE=$∠$CEA$（錯角）より、∠$CEA=$∠$CAE(=$∠$BAE)$となり、△$ACE$は、$AC=CE$の二等辺三角形となります。
一方、△$ABD$と△$ECD$が相似であることより$AB:CE=BD:DC$よって$AB:AC=BD:DC$
意味を理解したら問題を解いてみましょう。
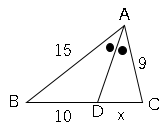
図で、$AD$は∠$A$の二等分線である。次の問いに答えなさい。
（１）$BD:DC$を求めなさい。（２）$x$の値を求めなさい。
不明点があればコメントよりどうぞ。