関数と正方形と円

問題９

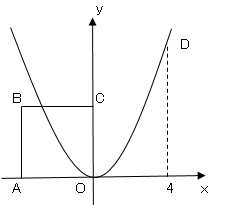
図のように$y=\displaystyle \frac{x²}{2}$のグラフと、$1$辺の長さが$a$の正方形$OABC$がある。点$A$は$x$軸上の点であり、点$A$の$x$座標は負である。
点$C$は$y$軸上の点であり、点$C$の$y$座標は正である。点$D$は関数$y=\displaystyle \frac{x²}{2}$のグラフ上の点であり、点$D$の$x$座標は$4$である。
ア、点$D$の座標を求めよ。
$CO=CD$のとき、次のイ、ウの問題に答えよ。
イ、$a$の値を求めよ。
ウ、∠$ODB$の大きさを求めよ。

ア、
点$D$の$x$座標は$4$なので、$y=\displaystyle \frac{x²}{2}$に代入して、
$y=\displaystyle \frac{4²}{2}$
$y=8$
点$D(4,8)$

イ、
$1$辺の長さが$a$の正方形$OABC$なので、$CO$の長さは$a$。
$CO=CD$より$CD=a$、$BC$の延長と点$D$から$x$軸に垂線を降ろした交点を$E$とする。

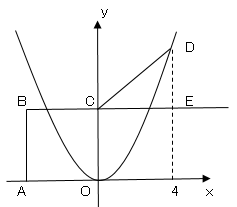
$DE$の長さは$DE=8-a$

三角形$CDE$において、三平方の定理より
$CD²=CE²+DE²$
$a²=4²+(8-a)²$
$a²=16+64-16a+a²$
$16a=16+64$
$16a=80$
$a=5$

ウ、
$CO=CD,CO=CB$なので、$3$点$B,O,D$は同一円周上にある。

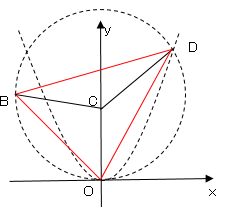
図で、円周角の定理より
∠$ODB=$∠$OCB×\displaystyle \frac{1}{2}$
∠$ODB=90×\displaystyle \frac{1}{2}=45$
∠$ODB=45°$