円の性質の練習問題1
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
4143 Views
2019年3月16日円の性質中学3年生
問1∠$x$の大きさを求めましょう。
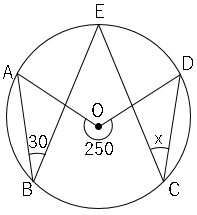
図のように補助線をひく。
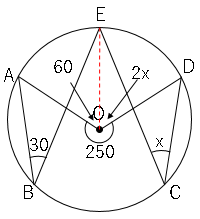
すると円周角の定理より、
∠$AOE=60°$、∠$EOD=2x°$
よって以下の式が成り立つ。
$360-250=60+2x$
$50=2x$
$x=25$
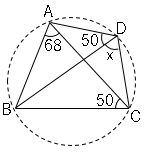
問2∠$x$の大きさを求めましょう。
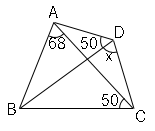
∠$ADB=$∠$ACB$より円周角の定理の逆が使える。以下の図のようになる。
よって、円周角の定理より
∠$x=68°$
問3図の$x$の値を求めましょう。
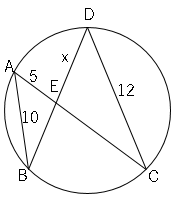
円周角の定理より、以下の図のようになる。
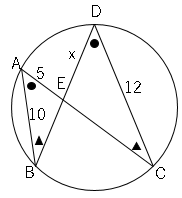
これより、△$ABE$∽△$DCE$
なので
$AB:AE=DC:DE$
$10:5=12:x$
$10x=60$
$x=6$
問4四角形$ABCD$の$4$つの頂点は円$O$の周上にあり、$EF$//$CD$である。このとき、△$ABC$∽△$EFD$を証明しましょう。
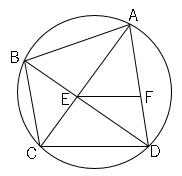
図のように、角が等しいものを図に入れ込む。
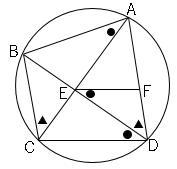
△$ABC$と△$EFD$において
円周角の定理より、
∠$ACB=$∠$EDF$・・・➀
∠$BAC=$∠$BDC$・・・➁
$EF$//$CD$より錯角が等しいので、
∠$BDC=$∠$FED$・・・➂
➁、➂より
∠$BAC=$∠$FED$・・・➃
➀、➃より
2角がそれぞれ等しいので、
△$ABC$∽△$EFD$
問5点$P$から円$O$に引いた接線$2$本を作図しましょう。
最終的にこのような図が書ければよい。
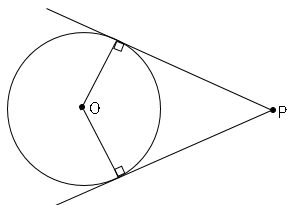
ポイントは
「円周角の定理の$90°$」を利用する。
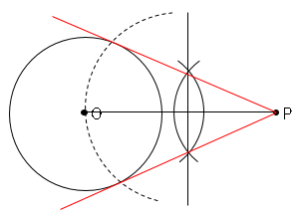
➀$OP$を結び、垂直二等分線で中心を求める。
➁中心と点$O$の半径分の円を描き、交点を求める。
➂交点と点$P$を結ぶ。
実際の受験問題を解いてみましょう。
受験問題
不明点があればコメント欄よりお願いします。























ディスカッション
コメント一覧
まだ、コメントがありません