円の性質
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
42479 Views
円周角の定理特徴は以下になります。
1.中心角は円周角の2倍である。∠$BOC=2$∠$BAC$
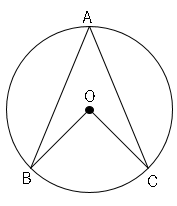
2.同じ弧$(BC)$に対する円周角は等しい。∠$BDC=$∠$BAC$
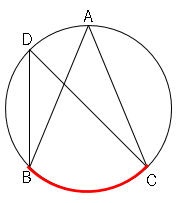
3.半円の弧$(BC)$に対する円周角は直角(90°)である。
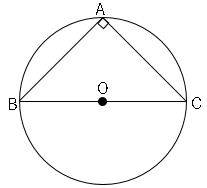
1.中心角は円周角の2倍である。∠$BOC=2$∠$BAC$

2.同じ弧$(BC)$に対する円周角は等しい。∠$BDC=$∠$BAC$

3.半円の弧$(BC)$に対する円周角は直角(90°)である。

では問題です。図で、∠$BAC=40°$のとき、∠$x$の値を求めなさい。
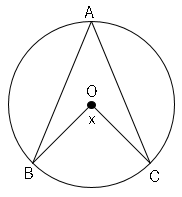
弧と円周角の関係特徴は以下になります。
1.等しい弧に対する円周角は等しい。$\stackrel{ \Large \frown }{ BC }=$$\stackrel{ \Large \frown }{ FE }$ならば∠$BAC=$∠$FDE$
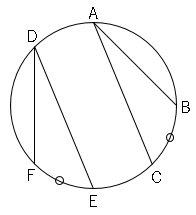
2.等しい円周角に対する弧は等しい。∠$BAC=$∠$FDE$ならば$\stackrel{ \Large \frown }{ BC }=$$\stackrel{ \Large \frown }{ FE }$
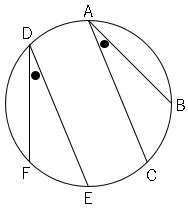
3.円周角の大きさは弧の長さに比例する。$\stackrel{ \Large \frown }{ BE }=2$$\stackrel{ \Large \frown }{ FE }$ならば∠$BAE=2$∠$FDE$
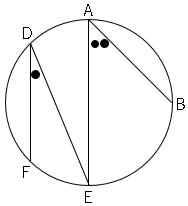
1.等しい弧に対する円周角は等しい。$\stackrel{ \Large \frown }{ BC }=$$\stackrel{ \Large \frown }{ FE }$ならば∠$BAC=$∠$FDE$

2.等しい円周角に対する弧は等しい。∠$BAC=$∠$FDE$ならば$\stackrel{ \Large \frown }{ BC }=$$\stackrel{ \Large \frown }{ FE }$

3.円周角の大きさは弧の長さに比例する。$\stackrel{ \Large \frown }{ BE }=2$$\stackrel{ \Large \frown }{ FE }$ならば∠$BAE=2$∠$FDE$

円周角の定理の逆名前の通り円周角の逆になります。
1.$2$点$P,Q$が直線$AB$について同じ側にあって、∠$APB=$∠$AQB$ならば、$4$点$A,B,P,Q$は$1$つの円周上にある。これはよく入試で出るので、必ず理解してください。差がつく問題です。
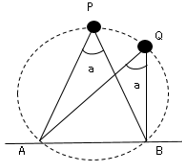
2.∠$APB=90°$のときは点$P$は$AB$を直径とする円周上にある。
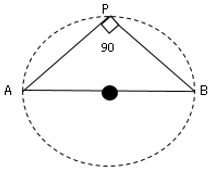
これらは主に相似を証明するときに使います。
1.$2$点$P,Q$が直線$AB$について同じ側にあって、∠$APB=$∠$AQB$ならば、$4$点$A,B,P,Q$は$1$つの円周上にある。これはよく入試で出るので、必ず理解してください。差がつく問題です。

2.∠$APB=90°$のときは点$P$は$AB$を直径とする円周上にある。

これらは主に相似を証明するときに使います。
円と接線の関係以下の特徴があります。
1.円の接線($m$)は接点を通る半径に垂直である。
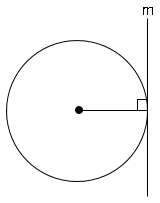
2.円外の点($B$)から、その円に引いた接線の長さ($BA=BC$)は等しい。
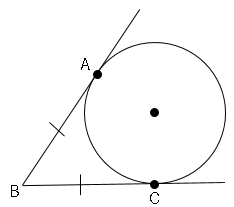
1.円の接線($m$)は接点を通る半径に垂直である。

2.円外の点($B$)から、その円に引いた接線の長さ($BA=BC$)は等しい。

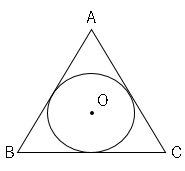
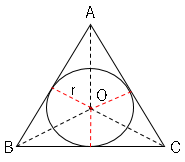
では問題です。図で、円$O$は△$ABC$の$3$辺に接している。$AB=13$,$BC=14$,$CA=15$、△$ABC$の面積が$84cm²$のとき、円$O$の半径は何$cm$ですか。
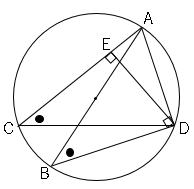
では問題です。図で、線分$AB$は円の直径であり、点$C$、$D$はこの円の周上にある。点$D$から線分$AC$に垂線をひき、その交点を$E$とする。このとき△$ABD$∽△$DCE$であることを証明せよ。
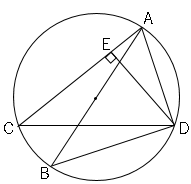
実際の受験問題を解いてみましょう。
受験問題
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
とても分かりやすかったです
ありがとう!
ありがたい
ありがとう!
図で表示されていたから、自分自身も分かりました。
良い問題も有難う御座います。
どういたしまして~