立体の線分の最短と最長

問題９

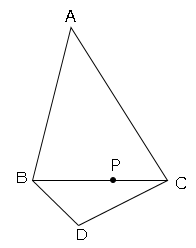
図のように、$BC=2cm､AC=3cm､$∠$ACB=60$°の三角形$ABC$と、$DC=\sqrt{3}cm$,∠$BDC=90$°の直角三角形$BDC$がある。点$P$が$BC$上を動くとする。
（１）ＡＰ＋ＰＤが最長になる場合の長さを求めなさい。
（２）ＡＰ＋ＰＤが最短になる場合の長さを求めなさい。
（３）点Ｐが辺ＢＣの中点であるとき、ＡＰ＋ＰＤの長さを求めなさい。
（４）ＡＰ＋ＰＤ＝４ｃｍのとき、ＡＰの長さを求めなさい。

方針

ＡＰ＋ＰＤが最長とは図より点Ｃの位置にＰがきたときである。

ＡＰ＋ＰＤが最短とは図より直線ＡＤ上にＰがあるときである。

点Ｐが辺ＢＣの中点であるとき、ＢＰ＝ＣＰ＝１ｃｍなので長さに注目する。

わからないものを文字で置く。

よってＡＣ＋ＣＤの長さを求めると$3+\sqrt{3}$

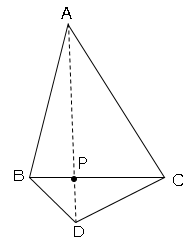
△ＢＤＣは３０°、６０°、９０°の直角三角形より、∠ＢＣＤ＝３０°となる。よって△ＡＤＣは∠ＡＣＤが９０度の直角三角形となる。よってＡＤの長さは３平方の定理より
$AD²=AC²+CD²$
$AD²=3²+\sqrt{3}²$
$AD=2\sqrt{3}$

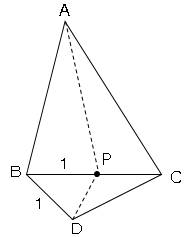
すると△ＢＤＰはＢＤ＝ＢＰの２等辺三角形で角度が（２）より６０度なので、△ＢＤＰは正三角形だとわかる。よってＤＰ＝１ｃｍ。
また、Ａから垂線を降ろし、ＢＣとの交点をＱとする。

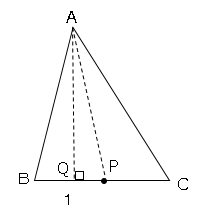
すると△ＡＱＣは３０°、６０°、９０°の直角三角形よりＱＣは
$AC:QC=2:1$
$3:QC=2:1$
$QC=\displaystyle \frac{3}{2}$

よって
$QP=\displaystyle \frac{3}{2}-1$
$QP=\displaystyle \frac{1}{2}$

またＡＱは
$AQ:QC=1:\sqrt{3}$
$AQ:\displaystyle \frac{3}{2}=1:\sqrt{3}$
$AQ=\displaystyle \frac{3\sqrt{3}}{2}$

これよりＡＰの長さは３平方の定理より
$AP²=AQ²+QP²$
$AP²=(\displaystyle \frac{3\sqrt{3}}{2})²+(\displaystyle \frac{1}{2})²$
$AP=\sqrt{7}$

これより求める長さは
$1+\sqrt{7}$

ＡＰ＝ａとすると、ＤＰ＝４－ａとなる。
△ＡＱＰに３平方の定理を用いてＱＰの長さは
$QP²=AP²-AQ²$
$QP²=a²-(\displaystyle \frac{3\sqrt{3}}{2})²$
$QP²=a²-\displaystyle \frac{27}{4}$･･･①

また、（３）より
$QC=\displaystyle \frac{3}{2}$
よってＢＱの長さは
$BQ=2-\displaystyle \frac{3}{2}$
$BQ=\displaystyle \frac{1}{2}$

またＢＤ＝１なので、△ＢＤＱは３０、６０、９０°の直角三角形となる。
△ＢＤＱに３平方の定理を用いてＱＰの長さは
$QP²=DP²-DQ²$
$QP²=(4-a)²-(\displaystyle \frac{\sqrt{3}}{2})²$
$QP²=a²-8a+16-\displaystyle \frac{3}{4}$･･･②

➀＝➁より
$a²-\displaystyle \frac{27}{4}=a²-8a+16-\displaystyle \frac{3}{4}$
$-6=-8a+16$
$a=\displaystyle \frac{11}{4}$