立体の体積の基本

問題１図のように、立体ＡＢＣＤ－ＥＦＧＨにおいて、面ＡＢＣＤと面ＥＦＧＨは１辺の長さがそれぞれ２ｃｍ,４ｃｍの正方形であり、この２つの面は平行である。また、それ以外の４つの面は、すべて台形でＡＥ＝ＢＦ＝ＣＧ＝ＤＨ＝３ｃｍである。
（１）辺ＡＢとねじれの位置にある辺をすべて求めよ。
（２）線分ＡＦの長さを求めよ。
（３）立体ＡＢＣＤ－ＥＦＧＨの体積を求めよ。

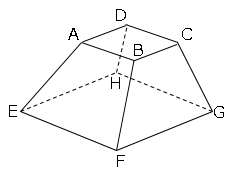
方針立体の問題は、部分的に取り出して考えるとわかりやすい。

台形ＡＢＦＥを取り出して考えてみる。

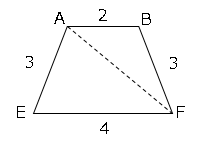
Ａから垂線を引き交点をＩとする。これで三平方の定理で求められる。

自分の知っている体積になるように補助線を引くと、

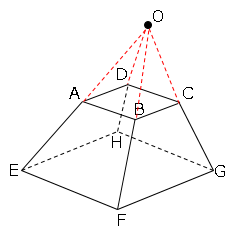
Ｏ－ＡＢＣＤとＯ－ＥＦＧＨは三角錐となる。
Ｏから面ＡＢＣＤとＥＦＧＨに垂線を引き高さを求める。

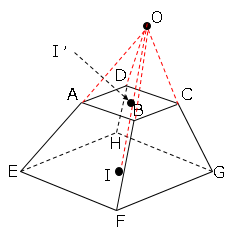
図のようにＩ,Ｉ’とする。高さを含む図を取り出す。

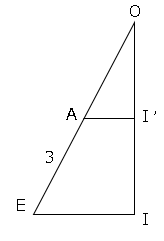
ここで△ＯＡＩ∽△ＯＥＩなので高さは求まる。
※ＡＩ’、ＥＩ、Ｉ’Ｉは三平方の定理で求まる。
求める体積はＯ－ＥＦＧＨからＯ－ＡＢＣＤを引けばよい。

よって辺ＥＨ、辺ＦＧ、辺ＤＨ、辺ＣＧ

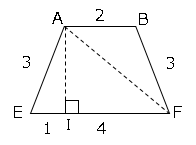
図より、△ＡＥＩに三平方の定理を用いて
$AI²=AE²-EI²$
$AI²=3²-1²$
$AI²=8$
次に△ＡＦＩに三平方の定理を用いて
$AF²=AI²+FI²$
$AF²=8+3²$
$AF=\sqrt{17}$
よって
$AF=\sqrt{17}$

まずＥＩの長さを求める。

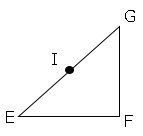
ＥＩの長さはＥＧの長さの半分なので、
ＥＧの長さを求める。
△ＥＧＦは特別な三角形(４５°、４５°、９０°)より
$EG=4\sqrt{2}$
よって
$EI=2\sqrt{2}$
次にＡＩ’を求める。

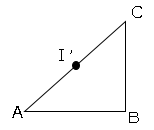
ＡＩ’の長さはＡＣの長さの半分なので、
ＡＣの長さを求める。
△ＡＢＣは特別な三角形(４５°、４５°、９０°)より
$AC=2\sqrt{2}$
よって
$AI’=\sqrt{2}$
最後にＩＩ’の長さを求める。
ＩＩ’を含む、図形を取り出すと。

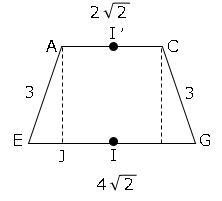
ＩＩ’はＡＪと同じ長さになる。
図より、△ＡＥＪに三平方の定理を用いて
$AJ²=AE²-EJ²$
$AJ²=3²-\sqrt{2}²$
$AJ=\sqrt{7}$
よって
$II’=\sqrt{7}$
これらを最初の図に書きこむと、

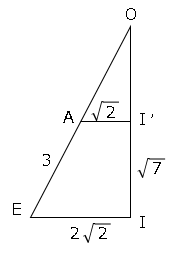
△ＯＡＩ∽△ＯＥＩなので
$AI’:EI=OI’:OI$
$\sqrt{2}:2\sqrt{2}=OI’:OI$
$1:2=OI’:OI$
$OI’=\sqrt{7}$
これよりＯ－ＡＢＣＤの体積は
$AB×BC×OI’÷3$
$=2×2×\sqrt{7}÷3$
$=\displaystyle \frac{4\sqrt{7}}{3}$
またＯ－ＥＦＧＨの体積は
$EF×FG×OI÷3$
$=4×4×2\sqrt{7}÷3$
$=\displaystyle \frac{32\sqrt{7}}{3}$
よって求める体積は
$\displaystyle \frac{32\sqrt{7}}{3}-\displaystyle \frac{4\sqrt{7}}{3}$
$=\displaystyle \frac{28\sqrt{7}}{3}$