三平方の定理の利用

問題１１

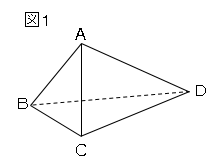
図１のように、三角錐ＡＢＣＤがある。

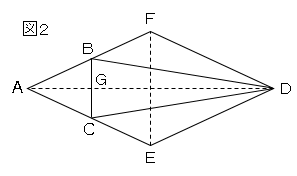
図２は図１の展開図である。
この展開図の四角形ＡＥＤＦはひし形で、ＡＤ＝８ｃｍ、ＥＦ＝６ｃｍで、線分ＡＤとＢＣの交点をＧとする。

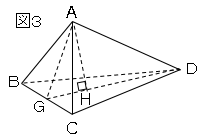
また、図の３はＡから垂線を降ろし、線分ＧＤとの交点をＨとしたものである。
（１）図２において、△ＡＢＣの面積は四角形ＡＥＤＦの面積の何倍か。
（２）図の３において、線分ＡＨの長さを求めなさい。

方針

点Ａ,Ｅ,Ｆは図１では重なっていることに注目する。

体積を求めてからやる方法、線分ＡＨを２つの方法で表す方法のどちらでやるのか？

ＡＢ＝ＢＦ、ＡＣ＝ＣＦとなる。
図２より、△ＡＢＣ∽△ＡＦＥなので
（∠Ａは共通、ＡＢ：ＡＦ＝ＡＣ：ＡＥ＝１：２）

面積比は
△$ABC:$△$AFE=1²:2²=1:4$
四角形ＡＥＤＦは△ＡＦＥの面積の２倍なので、
四角形ＡＥＤＦの面積比は８となる。
これより△ＡＢＣの面積は四角形ＡＥＤＦの面積の
$\displaystyle \frac{1}{8}$倍

体積を求めるには９０度の所を探すが・・・見当たらないので、線分ＡＨを２つの方法で出してみる。
つまりＡＧ、ＧＨの長さとＡＤ、ＤＨの長さを考える。
ＡＤとＦＥの交点をＩとおく。

ＡＧの長さは、△ＡＢＣ∽△ＡＦＥなので、
$AG:AI=1:2$
$AG:4=1:2$
$AG=2$
よって$GD=6$

図３でＡＤの長さはＦＤの長さと同じ、つまりＡＦの長さと同じとなる。ひし形の対角線は直角に交わる。
またＡＩ＝４、ＦＩ＝３なので特別な三角形より、
ＡＦ＝５
ＧＨ＝ｘとすると
△ＡＧＨに三角形の定理を用いて、
$AH²=AG²-GH²$
$AH²=4-x²$・・・➀

また
△ＡＤＨに三角形の定理を用いて、
$AH²=AD²-DH²$
$AH²=5²-(6-x)²$
$AH²=-x²+12x-11$・・・➁
➀＝➁より、
$4-x²=-x²+12x-11$
$x=\displaystyle \frac{-5}{4}$

これを➀に代入して
$AH²=4-(\displaystyle \frac{-5}{4})²$
$AH²=4-(\displaystyle \frac{-5}{4})²$
$AH=\displaystyle \frac{\sqrt{39}}{4}$