関数と相似と面積比の関係
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
5081 Views
問題1図のように関数$y=ax²(a>0)$・・・①のグラフ上に、$2$点$A、B$があります。
点$A$の$x$座標を$-2$、点$B$の$x$座標を$3$とします。点$O$は原点とします。次の問いに答えなさい。
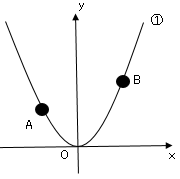
1.点$A$の$y$座標が$16$のとき、$a$の値を求めなさい。
2.$a=2$とします。➀について、$x$の値が$1$から$3$まで増加するときの変化の割合を求めなさい。
3.点$A$と$y$軸について対称な点を$C$とします。線分$AB$と$y$軸との交点を$D$とします。△$BCD$の面積が$10$のとき、$a$の値を求めなさい。
点$A$の$x$座標を$-2$、点$B$の$x$座標を$3$とします。点$O$は原点とします。次の問いに答えなさい。

1.点$A$の$y$座標が$16$のとき、$a$の値を求めなさい。
2.$a=2$とします。➀について、$x$の値が$1$から$3$まで増加するときの変化の割合を求めなさい。
3.点$A$と$y$軸について対称な点を$C$とします。線分$AB$と$y$軸との交点を$D$とします。△$BCD$の面積が$10$のとき、$a$の値を求めなさい。
1.
点$A$の$x$座標が$-2$、$y$座標が$16$なので、$y=ax²$に代入する。
$16=a×(-2)²$
$4a=16$
$a=4$
2.
変化の割合は$\displaystyle \frac{yの増加量}{xの増加量}$で求めることができる。よって
$\displaystyle \frac{2×3²-2×1}{3-1}$
$=\displaystyle \frac{18-2}{2}$
$=\displaystyle \frac{16}{2}$
$=8$
3.
線分$AC$と$y$軸との交点を$E$、点$B$から$y$軸に垂線を引きその交点を$F$とする。
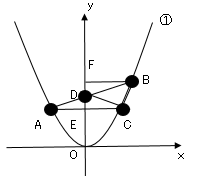
点$A,B$の座標は$y=ax²$に代入して点$A$の座標は$(-2,4a)$、点$B$の座標は$(3,9a)$、点$C$の座標は点$A$を$y$軸について対象移動させたので、点$C$の座標は$(2,4a)$
ここで△$ADE$と△$BDF$は相似なので($2$角がそれぞれ等しい)$AD:BD=AE:BF=2:3$
また、△$ADC$と△$DBC$は底辺をそれぞれ$AD、DB$とすると高さは共通になる。
よって、△$ADC$と△$DBC$の面積比は$2:3$となる。
また△$ACB$の面積は$4×5a÷2=10a$これより面積比から以下が成り立つ
$△ACB:△DBC=2+3:3$
$10a:10=5:3$
$30a=50$
$a=\displaystyle \frac{5}{3}$
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません