高さをうまく利用した体積の求め方
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
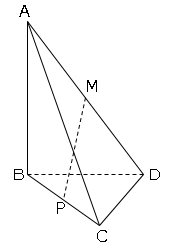
図１に示した立体Ａ－ＢＣＤはＡＢ＝８ｃｍ、ＢＣ＝ＢＤ＝６ｃｍ、∠ＡＢＣ＝∠ＡＢＤ＝９０°、∠ＣＢＤ＝６０°の三角すいである。辺ＡＤの中点をＭとする。辺ＢＣ上にある点をＰとし、点Ｍと点Ｐを結ぶ。
（１）点Ｐが辺ＢＣの中点となるとき、線分ＭＰの長さを求めよ。
（２）図２は図１において、辺ＡＣ上にあるを点Ｑとし、頂点Ｂと点Ｍ、頂点Ｂと点Ｑ、点Ｍと点Ｑ、点Ｐと点Ｑをそれぞれ結んだ場合を表している。
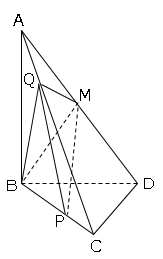
ＢＰ＝５ｃｍ、ＡＱ＝２ｃｍのとき、立体Ｍ－ＱＢＰの体積を求めなさい。
直接求めることはできないので、３平方の定理で求める。
平面ＢＣＤに平行な面をＭから引く。
（ＢＣＤが正三角形なので、使えるかもしれないから。）
Ｍから辺ＢＤに垂線を引き交点をＨとすると、以下の図になる。
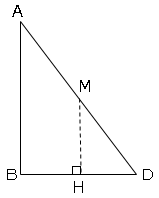
すると、△ＡＢＤ∽△ＭＨＤとなる。
（∠ＡＢＤ＝∠ＭＨＤ、∠Ｄは共通）
これより
$AB:MH=2:1$
$8:MH=2:1$
$MH=4$
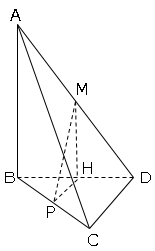
ここでＰ、Ｈを結ぶと、∠ＭＨＰ＝９０°となる。
（△ＢＣＤは同一平面上なので）
$BH:BD=BP:BC=1:2$より、
中点連結定理が成り立ち、ＰＨの長さはＣＤの半分
（ＢＣ＝ＣＤ＝６、∠ＣＢＤ＝６０°より△ＣＢＤは正三角形になる。）
よって$PH=3$
△ＰＭＨは特別な三角形より、
（別解：三平方の定理より、ＭＰ²＝ＭＨ²＋ＰＨ²を解けば求まる。）
ＭＰ＝５ｃｍ
図のようになり交点をそれぞれ置く。
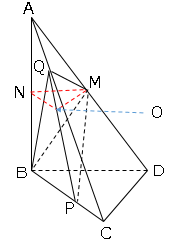
平面ＢＣＤに平行なので、△ＭＮＯは正三角形であり、ＭＮの長さは
中点連結定理より、ＭＮ＝３となる。
（ＡＮ＝ＮＢ、ＡＭ＝ＭＤなので中点連結定理が使える。）
ＭからＯＮに垂線を引き、交点をＲとする。
ＭＲの長さは特別な三角形より、
$\displaystyle \frac{3\sqrt{3}}{2}$
また、底面積は図のように考える。
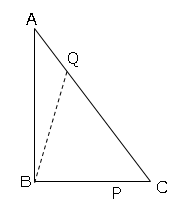
図より、△ＡＱＢと△ＣＱＢは高さが共通なので面積比は底辺の比に等しい。
よって△ＢＱＣの面積は
$\displaystyle \frac{4}{5}×24$
（△ＡＢＣの面積は６×８÷２＝２４）
また図より、
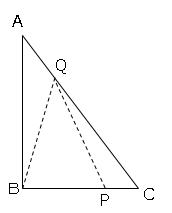
△ＢＱＰと△ＣＱＰは高さが共通なので面積比は底辺の比に等しい。
よって△ＢＱＰの面積は
$\displaystyle \frac{5}{6}×\displaystyle \frac{4}{5}×24$
$=16$
これより求める体積は
$16×\displaystyle \frac{3\sqrt{3}}{2}÷3$
$8\sqrt{3}$
不明点があればコメント欄よりお願いします。