底面積の利用
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
4868 Views
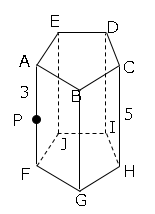
問題15図のような、底面が1辺2cmの正五角形で高さが5cmである正五角柱ABCDE-FGHIJがあり、辺AF上にAP=3cmとなる点Pがある。
(1)正五角柱ABCDE-FGHIJの側面上に点Pと点Hを最短の長さで結ぶ線を引くとき、その線の長さを求めなさい。
(2)正五角柱ABCDE-FGHIJの体積をScm³、五角錐P-FGHIJの体積をTcm³とする。このとき、2つの図形の体積の比S:Tを、最も簡単な整数の比で表しなさい。
(1)正五角柱ABCDE-FGHIJの側面上に点Pと点Hを最短の長さで結ぶ線を引くとき、その線の長さを求めなさい。
(2)正五角柱ABCDE-FGHIJの体積をScm³、五角錐P-FGHIJの体積をTcm³とする。このとき、2つの図形の体積の比S:Tを、最も簡単な整数の比で表しなさい。

方針
(1)の問題の考え方
図形の最短の長さは展開図を書く。
(2)の問題の考え方
底面積が共通なことに気付くと・・・。
展開図を書く。
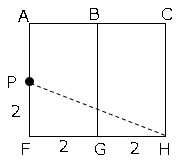
求める最短の長さはPHの長さと同じになる。
三角形PFHにおいて3平方の定理より、
$PH²=PF²+FH²$
$PH²=2²+4²$
$PH=2\sqrt{5}$
底面積は共通なので・・・
底面積をacm²とすると、体積はそれぞれ
$S=a×5$
$T=a×2÷3$
となる。よって、
$S:T=15:2$
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません