立体の動点と場合分け
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
点Pは、頂点Aを出発して、対角線AH,辺HG,GF,FE,EA上をA→H→G→F→E→Aの順に毎秒2cmの速さで動き、頂点Aに達したところで停止する。
点Qは、頂点Aを出発して、辺AB,BC上をA→B→C→Bの順に毎秒1cmの速さで動き、点Pが停止すると同時に停止する。
2点P,Qが同時に頂点Aを出発し、出発してからx秒後の三角錐PDAQの体積をycm³とする。ただし、x=0のとき、y=0とする。
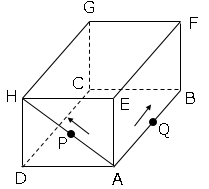
(1)点Pが対角線AH上にあるとき、
ア：xの変域を求めよ。
イ：x=2のときのyの変域を求めよ。
ウ：yをxの式で表せ。
(2)点Pが辺HG上にあるとき、xの変域を求めよ。また、そのときのyをxの式で表せ。
(3)5≦x≦9のとき、xの値に関係なくyの値は一定になることを示せ。
(4)三角錐PDAQの体積が4cm³となるとき何秒後か。
ア
$AH$の長さは特別な三角形より$AH=5cm$となる。
$P$は毎秒$2cm$で動くので、$x$の変域は
$0≦x≦2.5$
イ
図のような位置に点Pがある。点Pから垂線を引き交点をIとする。
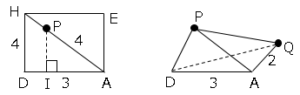
するとPIの長さは
$AP:AH=PI:HD$(△APIと△AHDは2角が等しいので相似)
$4:5=PI:4$
$PI=\displaystyle \frac{16}{5}$
となる。よって、三角錐の体積は
$y=3×2÷2×\displaystyle \frac{16}{5}×\displaystyle \frac{1}{3}$
$y=\displaystyle \frac{16}{5}$
ウ
上記同様にPIの長さは
$AP:AH=PI:HD$
$2x:5=PI:4$
$PI=\displaystyle \frac{8x}{5}$
となる。よって、三角錐の体積は
$y=3×x÷2×\displaystyle \frac{8x}{5}×\displaystyle \frac{1}{3}$
$y=\displaystyle \frac{4x²}{5}$
$x$の変域は
$2.5≦x≦5$
点$P$が辺$HG$上にあるので、高さは$4cm$で一定となる。
よって、三角錐の体積は
$y=3×x÷2×4×\displaystyle \frac{1}{3}$
$y=2x$
点$P$が辺$GF,FE$上にあるので、高さは$4cm$で一定となる。
また、点$Q$は辺$BC$上にあるので、底面積の高さは$5cm$で一定。
よって、三角錐の体積は
$y=3×5÷2×4×\displaystyle \frac{1}{3}$
$y=10$
これよりx,yの値に関係なく一定。
点Pが辺EA上にあるとき、$x$の変域は
$9≦x≦11$
となる。
するとAPの長さは$22-2x$
また、点Qは辺BC上にあるので、底面積の高さは5cmで一定。
よって、三角錐の体積は
$y=3×5÷2×(22-2x)×\displaystyle \frac{1}{3}$
$y=55-5x$
これより三角錐PADQの体積が4cm³になる可能性があるのは
➀$0≦x≦2.5$のとき、
$4=\displaystyle \frac{4x²}{5}$
$x=\sqrt{5}$
これは$x$の変域に合う。
➁$2.5≦x≦5$のとき、
$4=2x$
$x=2$これは$x$の変域に合わない。
➂$9≦x≦11$のとき、
$4=55-5x$
$x=\displaystyle \frac{51}{5}$これは$x$の変域に合う。
これより求める解は$x=\sqrt{5},\displaystyle \frac{51}{5}$
不明点があればコメント欄よりお願いします。