体積と三平方の定理

問題４

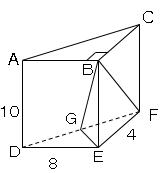
図のようにＡ,Ｂ,Ｃ,Ｄ,Ｅ,Ｆを頂点とし、∠ＤＥＦ＝９０°の直角三角形ＤＥＦを底面の１つとする三角柱がある。
辺ＤＦの中点をＧとし、４点Ｂ,Ｅ,Ｆ,Ｇを結んで三角錐Ｐをつくる。
辺ＤＥの長さを８ｃｍ、辺ＥＦの長さを４ｃｍ、辺ＡＤの長さを１０ｃｍとする。
（１）三角錐Ｐの体積を求めなさい。
（２）三角錐Ｐの辺ＢＧの長さを求めなさい。

方針立体の問題は、部分的に取り出して考えるとわかりやすい。

➀
体積を出すので、△ＥＦＧの面積を求める。
また、高さは図よりＢＥとなる。

➀
△ＢＥＧは直角三角形なのでＥＧの長さを求め、３平方の定理でＧＢを求める。

三角形ＤＥＦの面積は
$8×4÷2$
$=16$

△ＤＥＧと△ＦＧＥは底辺、高さが同じなので、△ＥＦＧの面積は
$16÷2$
$=8$

よって求める体積は
$8×10÷3$
$=\displaystyle \frac{80}{3}$

点Ｇが中点で、△ＤＥＦが直角三角形なので、点Ｇを中心とする円が３点Ｄ,Ｅ,Ｆを通る。
よって、ＧＤ＝ＧＦ＝ＧＥとなる。
ＦＤの長さを求める。
３平方の定理より、
$FD²=FE²+ED²$
$FD²=4²+8²$
$FD=4\sqrt{5}$

これより
$GE=2\sqrt{5}$

ゆえにＧＢは３平方の定理より、
$GB²=GE²+EB²$
$GB²=(2\sqrt{5})²+10²$
$GB=2\sqrt{30}$