関数と振り子の関係

問題１３

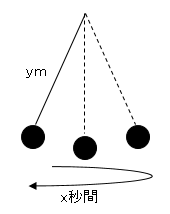
$1$往復するのに$x$秒かかる振り子の長さを$ym$とすると、$y=\displaystyle \frac{x²}{4}$という関係が成り立つ。$1$往復するのに$2$秒かかる振り子を振り子$A$とする。
ア、振り子$A$の長さを求めなさい。
イ、長さが$\displaystyle \frac{1}{4}m$の振り子$B$は、振り子$A$が$1$往復する間に何往復するか。

ア、
$1$往復するのに$2$秒かかるので、$x=2$を$y=\displaystyle \frac{x²}{4}$に代入して、
$y=1$
よって$1m$

イ、
長さが$\displaystyle \frac{1}{4}m$なので、
$y=\displaystyle \frac{1}{4}$を$y=\displaystyle \frac{x²}{4}$に代入して、
$\displaystyle \frac{1}{4}=\displaystyle \frac{x²}{4}$
$x=1$
よって$1$秒$A$の振り子は$1$往復するのに$2$秒かかり、$B$の振り子は$1$往復するのに$1$秒かかる。
よって$2$往復