関数と平行四辺形

問題１７

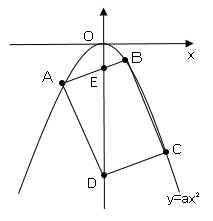
図のように、関数$y＝ax²$のグラフ上に$3$点$A$,$B$,$C$を、$y$軸上に点$D$を、四角形$ABCD$が平行四辺形となるようにし、四角形$ABCD$の辺$AB$と$y$軸との交点を$E$とする。点$A$の座標が$(-4,-4)$,点$B$の座標が$(2,p)$のとき、各問いを求めよ。
ア、$a,p$の値を求めよ。
イ、関数$y＝ax²$について$x$の変域が$-3≦x≦5$のとき、$y$の変域を求めよ。
ウ、$2$点$A,B$を通る直線の式を求めよ。
エ、点$D$の座標を求めよ。
オ、$x$軸上に点$F$をとり、△$CDF$をつくる。
△$CDF$の面積と△$AED$の面積が等しくなるとき、点$F$の座標を求めよ。
点$F$の$x$座標は正とする。

ア、$y=ax²$上に点$A$の座標を代入して、
$-4=a×(-4)²$
$a=\displaystyle \frac{-1}{4}$
また点$B$の座標は$x=2$を$y=\displaystyle \frac{-x²}{4}$に代入して、
$y=-1$
よって$p=-1$
イ、$\displaystyle \frac{-25}{4}≦y≦0$
ウ、$2$点$A,B$を通る直線の式を求める。$1$次関数$y=ax+b$に点$A,B$の値を代入
$\begin{equation}\begin{cases}\; -4=-4a+b･･･① \\\; -1=2a+b･･･②\end{cases}\end{equation}$
➀-②より
$-3=-6a$
$a=\displaystyle \frac{1}{2}･･･③$
③を②に代入して
$-1=1+b$
$b=-2$これより直線$AB$は$y=\displaystyle \frac{x}{2}-2$
エ、


四角形$ABCD$が平行四辺形なので、$AB$の傾き＝$CD$の傾きとなる。よって点$C,D$を求める。
点$C$の$x$座標を$c$とすると、$y$座標は$y=\displaystyle \frac{-x²}{4}$に代入して、$y=\displaystyle \frac{-c²}{4}$

点$D$の座標を求める。$a,b$の$y$座標の差は$3$、よって点$D$の$y$座標は$y=\displaystyle \frac{-c²}{4}-3$

$AB$の傾き＝$CD$の傾きより
$\displaystyle \frac{1}{2}=\displaystyle \frac{-\displaystyle \frac{c²}{4}-(\displaystyle \frac{c²}{4}-3)}{c-0}$
$\displaystyle \frac{1}{2}=\displaystyle \frac{3}{c}$
$c=6$

点$D$の$y$座標は
$y=\displaystyle \frac{-6²}{4}-3$
$y=-12$
よって点$D(0,-12)$
オ、△$AED$の面積を求める。$(12-2)×4÷2=20$
点$F$の座標を$(f,0)$とする。


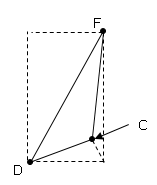
△$FDC$の面積は四角形から$3$つの三角形を引く。
$12×f-(f×12÷2)-$$(12×(f-6)÷2)-(f×(3)÷2)$
$=12f-(6f)-(6f-36)$$-(f×(3)÷2)$
$=36-\displaystyle \frac{3f}{2}$

これより
$20=36-\displaystyle \frac{3f}{2}$
$-16=-\displaystyle \frac{3f}{2}$
$f=\displaystyle \frac{32}{3}$
点$F$の座標は$(\displaystyle \frac{32}{3},0)$