三角形の面積と直線の式の求め方

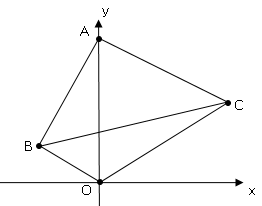
図で$O$は原点、$A$は$y$軸上の点、$B,C$は直線$y=\displaystyle \frac{x}{2}+4$上の点で、△$AOC$の面積は△$ABO$の面積の$2$倍、△$ABC$の面積は△$BOC$の面積の$3$倍である。点$B$の$x$座標が$-4$のとき、原点$O$を通り、四角形$ABOC$の面積を$2$等分する直線の式を求めよ。

原点を通り面積を$2$等分する直線の式は求めることができる。
よってこれをうまく使うことを考える。

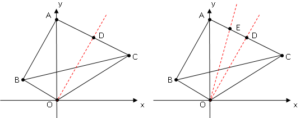
△$AOC$の面積は△$AOB$の面積の$2$倍なので、△$AOC$の面積を$2$等分する点$D$を求める。すると△$AOB$と△$AOD$と△$DOC$の面積は同じになる。更に△$AOD$の面積を$2$等分する点$E$を求めれば、直線$OE$が四角形$ABOC$の面積を$2$等分する直線となる。

➀面積との関係から各点の座標を求める。
②点$D$の座標を求める。
③点$E$の座標を求めて直線の式を出す。

点$B$の$x$座標は$-4$より直線$y=\displaystyle \frac{x}{2}+4$に代入して、
$y=\displaystyle \frac{-4}{2}+4$
$y=-2+4$
$y=2$
よって点$B$の座標は$(-4,2)$


△$AOC$の面積は△$AOB$の$2$倍より底辺を$AO$、高さが$2$倍になればよい。よって高さは$4×2$の$8$($x$座標)となる。これを直線$y=\displaystyle \frac{x}{2}+4$に代入して、
$y=\displaystyle \frac{8}{2}+4$
$y=4+4$
$y=8$
よって点$C$の座標は$(8,8)$


直線$BC$と$y$軸の交点を$F$とする。△$ABC$の面積は△$BOC$の$3$倍より底辺を$BC$、高さが$3$倍になればよい。よって
$OF:FA=1:3$
$4:FA=1:3$
$FA=12$
よって点$A$の座標は$(0,16)$

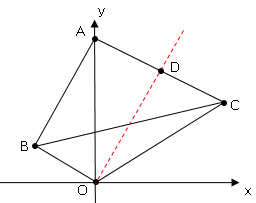
点$D$の座標は$(\displaystyle \frac{0+8}{2},\displaystyle \frac{16+8}{2})$よって点$D$の座標は$(4,12)$

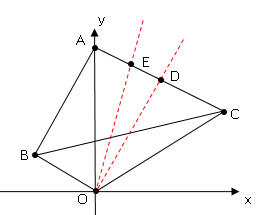
点$E$の座標は$(\displaystyle \frac{0+4}{2},\displaystyle \frac{16+12}{2})$よって点$D$の座標は$(2,14)$これより直線の式は$y=ax$に代入して
$14=2a$
$a=7$
よって
$y=7x$