台形と平行の証明問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
17245 Views
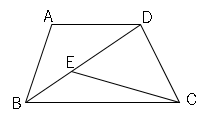
問題１６図のように、$AD//BC$の台形$ABCD$があり、∠$BCD=$∠$BDC$である。
また、対角線$BD$上に点$E$があり、∠$ABD=$∠$ECB$である。
このとき$AB=EC$を証明しましょう。
また、対角線$BD$上に点$E$があり、∠$ABD=$∠$ECB$である。
このとき$AB=EC$を証明しましょう。
方針
平行だから角度に注目する。
三角形の合同を証明する。
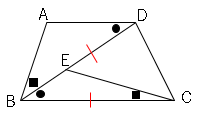
△$ABD$と△$ECB$において
仮定より、∠$ABD=$∠$ECB$・・・➀
∠$BCD=$∠$BDC$より△$BCD$は二等辺三角形なので、
$BD=CB$・・・➁
$AD//BC$より錯角が等しいので、
∠$ADB=$∠$EBC$・・・➂
➀、➁、➂より
$1$辺とその両端の角がそれぞれ等しいので、
△$ABD≡$△$ECB$
対応する辺はそれぞれ等しいので、$AB=EC$
不明点があればコメント欄よりお願いします。