接線と円と合同の証明問題

問題１５図$1$で$2$つの直線$ℓ,m$は、点$O$を中心とする円にそれぞれ点$P,Q$で接し、点$A$で交わっている。
直線$ℓ$上に点$R$を、点$A$に対して点$P$と反対側にとり、∠$QAR$を$45°$より大きく$90°$より小さい角とする。
点$O$と点$A$、点$O$と点$P$、点$O$と点$Q$をそれぞれ結ぶ。

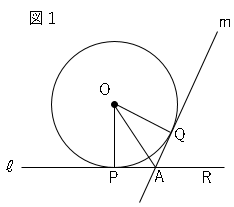
（１）∠$QAR=70°$のとき、∠$AOQ$の大きさは何度ですか。
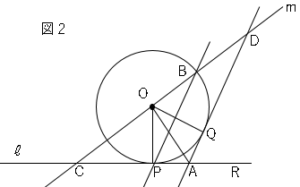
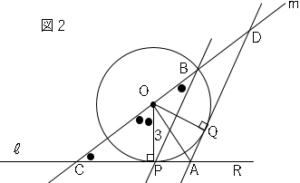
（２）図$2$は図$1$において、点$P$を通り直線$m$に平行な直線と円$O$との交点のうち、点$P$と異なる点を$B$、$2$点$O,B$を通る直線と$2$つの直線$ℓ,m$との交点をそれぞれ$C,D$とし$PB=PC$とする。
問１、△$OPC≡$△$OQD$を証明しましょう。
問２、円$O$の半径が$3cm$のとき、△$OAC$の面積を求めましょう。

方針

（１）

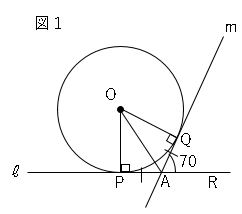
接線と円の関係より、∠$OPA=$∠$OQA=90°$
また、$AP=AQ$となる。
△$OPA≡$△$OQA$なので
（斜辺とその他の一辺がそれぞれ等しい）

∠$QAP$
$=180-70$
$=110°$

∠$OAQ$
$=110÷2$
$=55$

これより
∠$AOQ$
$=180-90-55$
$=35°$

問１

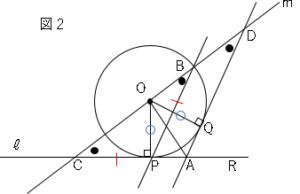
△$OPC$と△$OQD$において、
円の半径より$OP=OQ$・・・➀
円と接線の関係より、
∠$OPC=$∠$OQD=90°$・・・➁
$CP=PB$より△$CPB$は二等辺三角形なので、
∠$PCB=$∠$PBC$・・・➃
$PB//AD$より同位角が等しいので、
∠$PBC=$∠$QDO$・・・➄

➃、➄より∠$PCB=$∠$QDO$・・・➅
三角形の内角の和は$180°$であり、
➁と➅より
∠$POC=$∠$QOD$・・・➆
➀、➁、➆より
$1$辺とその両端の角がそれぞれ等しいので、
△$OPC≡$△$OQD$

問２

∠$PBC=a°$とすると、
円周角の定理より、
∠$COP=2a°$
また△$CPB$は二等辺三角形なので、
∠$PCB=a°$

これより△$POC$の内角の和は$180°$より
$180=a+2a+90$
$a=30°$
これより△$OPC$は$30,60,90°$の特別な三角形なので、
$CP=3\sqrt{3}$

また、∠$POC=$∠$QOD=60°$なので
∠$POQ=60°$
ゆえに∠$POA=30°$
これより△$OPA$は$30,60,90°$の特別な三角形なので、
$1:\sqrt{3}=PA:3$
$PA=\sqrt{3}$

求める面積は
$CA×OP÷2$
$=4\sqrt{3}×3÷2$
$=6\sqrt{3}$