平行四辺形の合同の証明と角度を求める問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
15500 Views
問題１０図のように、平行四辺形ＡＢＣＤがあり、点Ｅは辺ＢＣ上の点で、ＡＢ＝ＡＥである。
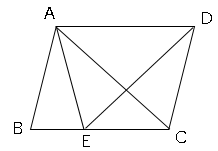
（１）△ＡＢＣ≡△ＥＡＤを証明しなさい。
（２）∠ＢＡＥ＝４０°、ＡＣ⊥ＤＥのとき、∠ＣＡＥの大きさを求めよ。
（１）△ＡＢＣ≡△ＥＡＤを証明しなさい。
（２）∠ＢＡＥ＝４０°、ＡＣ⊥ＤＥのとき、∠ＣＡＥの大きさを求めよ。
方針
平行四辺形の特徴を考えると錯角と対応する辺はそれぞれ等しい。
（１）平行四辺形の特徴を考える
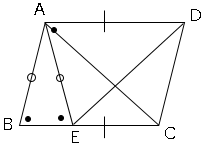
（１）△ＡＢＣと△ＥＡＤにおいて、
仮定よりＡＢ＝ＥＡ・・・➀
平行四辺形よりＢＣ＝ＡＤ・・・➁
△ＡＢＥは二等辺三角形より、∠ＡＢＣ＝∠ＡＥＢ
また、平行四辺形より∠ＡＥＢ＝∠ＥＡＤ
よって∠ＡＢＣ＝∠ＥＡＤ・・・➂
➀、➁、➂より
２辺とその間の角がそれぞれ等しいので、
△ＡＢＣ≡△ＥＡＤ
（２）（１）を使うと予想してそれぞれの角を求める。
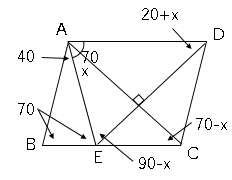
∠ＣＡＥ＝ｘとすると、∠ＡＥＤ＝９０－ｘ
∠ＢＡＥ＝４０°なので、∠ＡＥＢ＝∠ＡＢＥ＝７０°
平行四辺形なので∠ＡＥＢ＝∠ＥＡＤ＝７０°
これより∠ＡＤＥ=１８０－７０－（９０－ｘ）＝２０＋ｘ
また、∠ＡＣＢ＝１８０－４０－ｘ－７０＝７０－ｘ
（１）より
∠ＡＣＢ＝∠ＥＤＡ
７０－ｘ＝２０＋ｘ
ｘ＝２５°
不明点があればコメント欄よりお願いします。