辺の比と三角形の面積比と証明問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
また、線分$BD$上に点$F$をとり、線分$AD$上に$AC:AE=BF:DG$となる点$G$をとる。
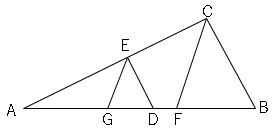
（１）△$BCF$∽△$DEG$を証明しましょう。
（２）図$2$は図$1$の辺$AC$上に、$DE//FH$となるように点$H$をとったものである。
$AG:GD=3:2$のとき、△$AFH$の面積は△$FBC$の面積の何倍ですか。
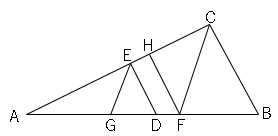
（１）
△$BCF$と△$DEG$において、
$BC//DE$なので同位角が等しいので、
∠$CBF=$∠$EDG$・・・➀
仮定より、$AC:AE=BF:DG$・・・➁
△$ADE$∽△$ABC$なので、
（∠$CBF=$∠$EDG$、∠$A$は共通）
$AC:AE=CB:ED$・・・➂
➁、➂より
$BF:DG=CB:ED$・・・➃
➀、➃より
$2$辺の比とその間の角がそれぞれ等しいので、
△$BCF$∽△$DEG$
（２）
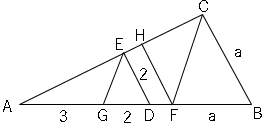
仮定より$AG:GD=3:2$で
$FB=a$とすると、
$CB=a$、$ED=2$
△$ADE$∽△$ABC$より
$AD:DE=AB:BC$
$5:2=AB:a$
$AB=\displaystyle \frac{5a}{2}$
これより、
$AF=\displaystyle \frac{5a}{2}-a$
$=\displaystyle \frac{3a}{2}$
また、△$AFH$∽△$ABC$なので
相似比は$\displaystyle \frac{3a}{2}:\displaystyle \frac{5a}{2}$
よって面積比は$(\displaystyle \frac{3a}{2})²:(\displaystyle \frac{5a}{2})²$
ゆえに△$AFH:$△$ABC=9:25$
また△$FBC$と△$ABC$の面積は高さが共通なので、
面積比は底辺の長さとなる。
△$ABC:$△$FBC=\displaystyle \frac{5a}{2}:a$
△$ABC:$△$FBC=5:2$
△$ABC=\displaystyle \frac{5}{2}×$△$FBC$
△$AFH:$△$ABC=9:25$なので、
△$AFH:\displaystyle \frac{5}{2}×$△$FBC=9:25$
$\displaystyle \frac{45}{2}×$△$FBC=25×$△$AFH$
$9×$△$FBC=10×$△$AFH$
△$AFH=\displaystyle \frac{9}{10}×$△$FBC$
これより△$AFH$は△$FBC$の$\displaystyle \frac{9}{10}$倍
不明点があればコメント欄よりお願いします。