三角形の相似・合同の証明問題と面積比と相似比の問題

問題３図のように、線分ABを直径とする円Oの円周上に点Cをとり、△ABCをつくる。
∠CABの二等分線と線分BC、円Oとの交点をそれぞれD,Eとし、線分CEをひく。
点Dから線分ACに平行な直線を引き、点Aを接点とする円Oの接線との交点をFとし、線分ABと線分DFの交点をGとする。
ただし、点Eは点Aと異なる点とする。

(1)△ACE∽△CDEを証明しなさい。
(2)△AGF≡△DGBを証明しなさい。
(3)AB＝10cm,AC=4cmのとき、線分AGの長さを求めよ。
また、△CDEと△AGFの面積比を整数比で表せ。

方針

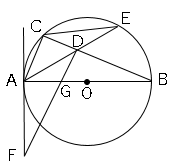
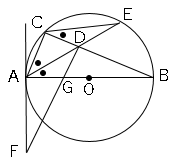
仮定：∠CAD＝∠DAG
円周角の定理：∠DCE＝∠DAG
∠Eは共通

証明
△ACEと△CDEにおいて、
仮定より∠CAD＝∠DAG・・・➀
円周角の定理より、
∠DCE＝∠DAG・・・➁
➀、➁より
∠CAD＝∠DCE・・・➂
∠Eは共通・・・➃

➂、➃より2角がそれぞれ等しいので、
△ACE∽△CDE

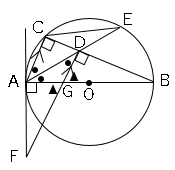
接点：∠FAG＝90°
円周角の定理：∠ACB＝90°
AC//FD(同位角)：∠GDB＝90°

仮定：∠CAD＝∠DAG
AC//FD(錯角)：∠CAD＝∠GDA
これより二等辺三角形：AG=GD
対頂角：∠AGF＝∠DGB

証明
△AGFと△DGBにおいて、
対頂角より∠AGF＝∠DGB・・・➀

点Aは接点なので∠FAG=90°・・・➁
円周角の定理より∠BCA＝90°
また、AC//FDで、同位角は等しいので、
∠BCA＝∠BDG＝90°・・・➂
➁と➂より∠FAG＝∠BDG・・・➃

仮定より、∠CAD＝∠DAG・・・➄
AC//FDで、錯角は等しいので、
∠CAD＝∠GDA・・・➅
➄、➅より∠DAG＝∠GDAの二等辺三角形なので、
AG=GD・・・➆

➀、➃、➆より
一辺とその両端の角がそれぞれ等しいので、
△AGF≡△DGB

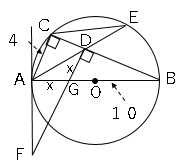
(2)よりAG=DGなのでGDの長さを求める。
△ACB∽△GDB（２角が等しい）
なのでDGが求まる。

$AG=DG=x$とすると、
△ACB∽△GDBなので、
$AC:GD=AB:GB$
$4:x=10:10-x$
$x=\displaystyle \frac{20}{7}$

△CDE∽ADB(円周角の定理より２角が等しい)
CDとADの長さを求めれば、面積比が出せる。
また、△ADGと△GDBは高さが等しいので、底辺の比が面積比になる。

三平方の定理より
$BD²=GB²-GD²$
$BD²=(\displaystyle \frac{50}{7})²-(\displaystyle \frac{20}{7})²$
$BD=\displaystyle \frac{10\sqrt{21}}{7}$

また、三平方の定理より
$BC²=AB²-AC²$
$BC²=(10)²-(4)²$
$BC=2\sqrt{21}$

これより
$CD=2\sqrt{21}-\displaystyle \frac{10\sqrt{21}}{7}$
$=\displaystyle \frac{4\sqrt{21}}{7}$

また、三平方の定理より
$AD²=AC²+CD²$
$AD²=(4)²+(\displaystyle \frac{4\sqrt{21}}{7})²$
$AD=\displaystyle \frac{4\sqrt{70}}{7}$

これより
△CDEと△ADBの面積比は
$CD²:DA²$
$=(\displaystyle \frac{4\sqrt{21}}{7})²:(\displaystyle \frac{4\sqrt{70}}{7})²$
$=3:10$

また、△ADGと△GDBは高さが等しいので、底辺の比が面積比になるので、
$AG:GB=\displaystyle \frac{20}{7}:\displaystyle \frac{50}{7}$
$AG:GB=2:5$

これより
△CDEの面積を$1$とすると
△ADBの面積は$\displaystyle \frac{10}{3}$
$AG:GB＝2:5$なので、

△GDBの面積は
$\displaystyle \frac{10}{3}×\displaystyle \frac{5}{7}$
$=\displaystyle \frac{50}{21}$

よって△$CDE：$△$GDB=21:50$
なので△$CDE:$△$AGF=21:50$