三角形と円を利用した相似の証明問題と面積比と線分の長さ
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
（１）△ＡＤＥ∽△ＢＤＦを証明しなさい。
（２）ＢＣ＝３ｃｍ、△ＡＤＥと△ＢＤＦの面積比を２：１とする。線分ＡＣの長さと△ＢＤＦの面積を求めよ。
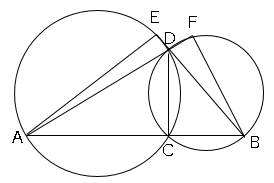
△ＡＤＥと△ＢＤＦにおいて、
対頂角より、∠ＡＤＥ＝∠ＢＤＦ・・・➀
垂線より∠ＤＣＢ＝９０°なので、線分ＢＤは円の直径なので、円周角の定理より∠ＢＦＤ＝９０°
また、∠ＡＣＤ＝９０°なので、線分ＡＤは円の直径なので、円周角の定理より∠ＡＥＤ＝９０°
よって∠ＡＥＤ＝∠ＢＦＤ・・・➁
➀、➁より２角がそれぞれ等しいので、△ＡＤＥ∽△ＢＤＦ
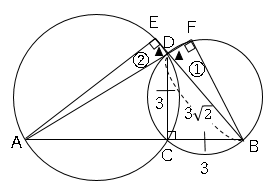
（１）
△ＣＢＤは４５、４５、９０°の特別な三角形なので、
$BD=3\sqrt{2}$
△ＡＤＥと△ＢＤＦの面積比は
$2:1$なので、相似比は
$\sqrt{2}:1$
よって
$AD:BD=\sqrt{2}:1$
$AD:3\sqrt{2}=\sqrt{2}:1$
$AD=6$
△ＣＤＡに三平方の定理より、
$AC²=AD²-DC²$
$AC²=6²-3²$
$AC=3\sqrt{3}$
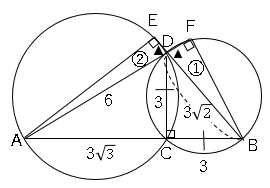
∠ＤＡＣ＝３０°、∠ＣＤＡ＝６０°、∠ＣＤＢ＝∠ＣＢＤ＝４５°より
∠ＡＤＥ＝７５°ゆえに∠ＥＡＤ＝１５°
これより△ＥＡＢは４５、４５、９０°の三角形になる。
よって
$AE:AB=1:\sqrt{2}$
$AE:(3+3\sqrt{3})=1:\sqrt{2}$
$AE=\displaystyle \frac{3\sqrt{6}+3\sqrt{2}}{2}$
これよりＤＥの長さは
$DE=EB-DB$
$DE=\displaystyle \frac{3\sqrt{6}+3\sqrt{2}}{2}-3\sqrt{2}$
$DE=\displaystyle \frac{3\sqrt{6}-3\sqrt{2}}{2}$
これより△ＡＤＥの面積は
$AE×DE÷2$
$=(\displaystyle \frac{3\sqrt{6}+3\sqrt{2}}{2})×(\displaystyle \frac{3\sqrt{6}-3\sqrt{2}}{2})÷2$
$=\displaystyle \frac{9}{2}$
△ＡＤＥと△ＢＤＦの面積比を２：１なので△ＢＤＦの面積は
$\displaystyle \frac{9}{4}$
不明点があればコメント欄よりお願いします。