作図と面積比の関係
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
5277 Views
問題7
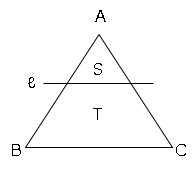
図のように、△ABCを辺BCと平行な直線ℓで2つに分けた時、上の三角形をS、下の台形をTとする。
SとTの面積比が1:3となるように直線ℓを作図せよ。
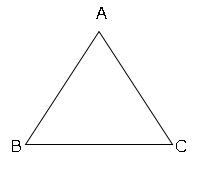

図のように、△ABCを辺BCと平行な直線ℓで2つに分けた時、上の三角形をS、下の台形をTとする。
SとTの面積比が1:3となるように直線ℓを作図せよ。

方針最終的に求める点を作図してから、何をすればいいか考える。
まず平行線を引く。

面積比が出ているので、相似な三角形を探す。(点D,Eを図のようにする。)
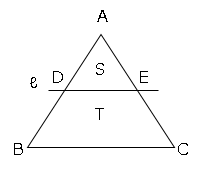
△ADE∽△ABCで面積比は、
1:1+3=1:4
よって相似比は1:2となる。
またAD:AB=1:2なので、
AD:DB=1:1
同様にAE:EC=1:1
つまり線分ABの垂直二等分線でできた点Dと、
線分ACの垂直二等分線でできた点Eを結べばよい。
まず平行線を引く。

面積比が出ているので、相似な三角形を探す。(点D,Eを図のようにする。)

△ADE∽△ABCで面積比は、
1:1+3=1:4
よって相似比は1:2となる。
またAD:AB=1:2なので、
AD:DB=1:1
同様にAE:EC=1:1
つまり線分ABの垂直二等分線でできた点Dと、
線分ACの垂直二等分線でできた点Eを結べばよい。
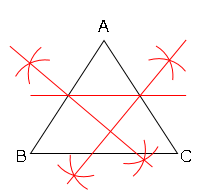
➀線分ABの垂直2等分線を引く。
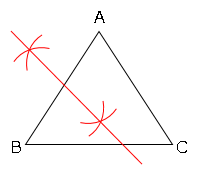
⓶線分ACの垂直2等分線を引き、交点を結ぶ。
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません