平行と三角形の合同
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
対頂角
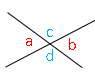
図のように２直線が交わっていて、４つの角度ができあがる。
∠ａ＝∠ｂ、∠ｃ＝∠ｄのように向かい合っている角を対頂角という。
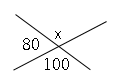
では問題です。図の$x$の角度を求めましょう。
同位角と錯角
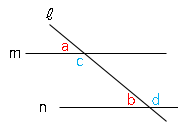
図のような２直線の平行線$m,n$があり、直線$ℓ$が交わっています。このとき、
∠$a$と∠$b$の関係を同位角といい、∠$a=$∠$b$
∠$c$と∠$d$の関係を錯角といい、∠$c=$∠$d$
平行線と同位角・錯角の関係
２つの直線に１つの直線が交わっているとき、同位角or錯角が等しければ、２つの直線は平行
※図の場合は同位角が等しい。
２つの平行な直線に１つの直線が交わっているとき、同位角は等しく・錯角も等しい
意味を理解したら問題を解いてみましょう。
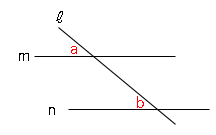
図の∠a,bの値を求めなさい。
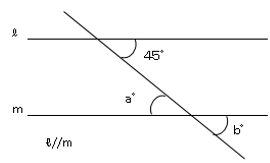
更にもう一問解いてみましょう。
図で、∠$a+$∠$b$＝$180°$ならば、$m$//$n$を示しましょう。
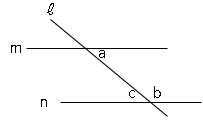
外角と内角の関係
△$ABC$の辺$BC$を延長した直線上に点$D$とする。
このとき、∠$ACD$を外角といい、∠$ABC$、∠$ACB$、∠$CAB$を内角という。
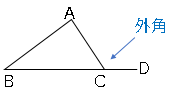
三角形の場合内角の和は$180°$、外角は∠$ACD=$∠$ABC+$∠$CAB$
意味を理解したら問題を解いてみましょう。
図の∠$x,y$の値を求めなさい。
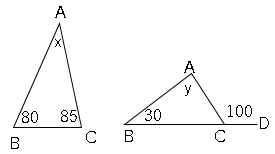
角度の名前
$0°$より大きく$90°$より小さい角を鋭角、$90°$より大きく$180°$より小さい角を鈍角といいます。
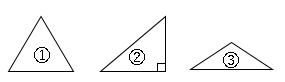
➀３つの角がすべて鋭角の三角形を鋭角三角形といいます。
➁１つの角が直角の三角形を直角三角形といいます。
➂１つの角が鈍角の三角形を鈍角三角形といいます。
多角形の内角の和と外角の和
$n$角形の内角の和は$180°×(n-2)$($n=3,4,5・・・$)
$n$角形の外角の和は$360°$（三角形でも四角形でも同じ$360°$）
簡単に説明すると、
三角形の内角の和は$180°$
四角形の内角の和は$180×2=360°$
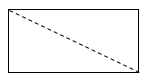
なぜなら図のように三角形が$2$つで切るので内角の和は$180°×2$
五角形の内角の和は$180×3=540°$
・・・
$n$角形の内角の和は$180(n-2)$
$n$角形の内角の和＋$n$角形の外角の和＝$180×n$
$180(n-2)$＋$n$角形の外角の和＝$180×n$
$n$角形の外角の和＝$360°$
意味を理解したら問題を解いてみましょう。
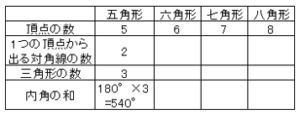
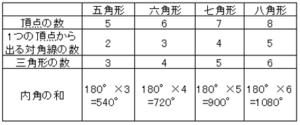
図の表の値を求めなさい。
合同な図形の性質
・合同な図形では、対応する線分の長さや角の大きさはそれぞれ等しい。
・「$≡$」は合同を表す記号である。
この記号を使うときは、対応する頂点の順に並べる。
例：△$ABC≡$△$DEF$
三角形の場合だけ△で表す。
では問題を解いてみましょう。
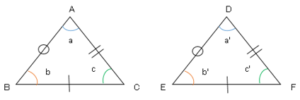
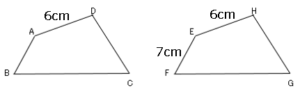
図は合同な図形である。
（１）合同であることを記号$≡$を使って表しましょう。
（２）∠$A$に対応する角はどれですか。
（３）辺$AB$は何$cm$ですか。
三角形の合同の条件
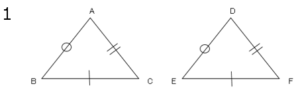
$1$.$3$組の辺がそれぞれ等しい。
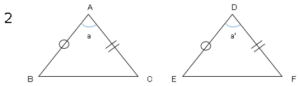
$2$.$2$組の辺とその間の角がそれぞれ等しい。
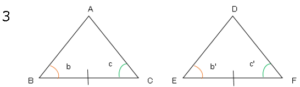
$3$.$1$組の辺とその両端の角がそれぞれ等しい。
では問題を解いてみましょう。
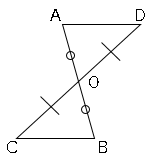
図で、同じ印の線分の長さや角は同じ大きさである。このとき、合同な三角形を記号を使って表し、その時に使った三角形の合同条件も書きなさい。
不明点があればコメントよりどうぞ。