規則性とカードの和の問題

問題１０$1$から$100$までの自然数が$1$つずつ書かれた$100$枚のカードがある。
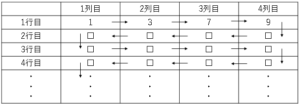
まず、この$100$枚のカードの中から$2$の倍数がかかれたカードを取り除き、残ったカードの中から$5$の倍数がかかれたカードを取り除く。
次に、表のように残ったカード全部を、カードに書かれた数が小さいものから順に$1$行目の$1$列目から矢印に沿って並べていく。
（１）$2$行目の$1$列目に並べたカードに書かれている数を書きましょう。
（２）$1$行目の$1$列目、$2$行目の$1$列目、$3$行目の$1$列目、$4$行目の$1$列目のカードの和を求めましょう。
（３）並べたカードの枚数は何枚ですか。
（４）並べたカード全部の和を求めましょう。

方針

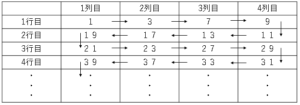
（１）
表より$19$
（２）
表より
$1+19+21+39$
$=80$

（３）

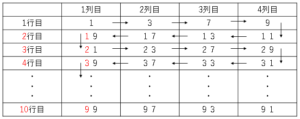
表の赤部分に注目すると、$2$行目で$1$、$3$行目で$2$、$4$行目で$3$、・・・なので$10$行目で$9$となる。
よってカードの枚数は
$4×10$
$=40$枚
（４）

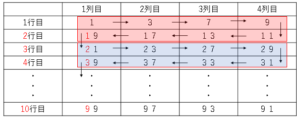
赤枠について考える。
前後を足すと$20$になり、それが$4$つあるので、赤枠の合計は$20×4$
青枠について考える。
前後を足すと$60$になり、それが$4$つあるので、青枠の合計は$60×4$
$5$行目と$6$行目の前後を足すと、$100$となる。それが$4$つあるので、$100×4$

これより$40$ずつ大きくなっていることがわかるので、
全部を足すと
$4×(20+60+100+140+180)$
$=2000$