オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
17703 Views
2018年3月19日確率中学2年生
問1
1枚の10円硬貨を2回投げる時、以下の確率を求めよう。
(1)2回とも表が出る確率
(2)表が1回だけ出る確率
(3)少なくとも1回は裏が出る確率
樹形図を書いて求めた方が早く、正確なので樹形図を書く。

(1)樹形図より、
$\displaystyle \frac{1}{4}$
(2)樹形図より、$\displaystyle \frac{2}{4}=$
$\displaystyle \frac{1}{2}$
(3)樹形図より、
$\displaystyle \frac{3}{4}$
【別解】少なくとも1回は裏なので、(1―表が2回出る確率)で求める。このやり方は覚えておくと便利です。
$1-\displaystyle \frac{1}{4}=$
$\displaystyle \frac{3}{4}$
問2
2つのサイコロを1回投げる時、以下の確率を求めよう。
(1)出る目の数の和が4になる確率
(2)出る目の数の和が6になる確率
(3)出る目の数の積が20以下になる確率
サイコロ2個までは、表を書いた方が一番早い。サイコロの目は1から6までなので以下の表になる。
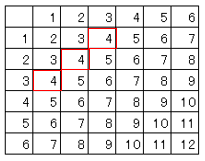
(1)$\displaystyle \frac{3}{36}=$
$\displaystyle \frac{1}{12}$
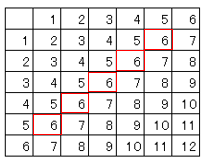
(2)
$\displaystyle \frac{5}{36}$
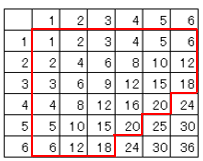
(3)$\displaystyle \frac{30}{36}=$
$\displaystyle \frac{5}{6}$
問3
袋の中に赤玉3個と白玉2個が入っている。同時に2個取り出すときに以下の確率を求めよう。
(1)2個とも赤玉の確率
(2)取り出した玉の1つが赤、もう1つは白の確率
(3)取り出した玉に白玉が含まれる確率
赤玉をR1,R2,R3とし、白玉をW1,W2とすると、樹形図より。
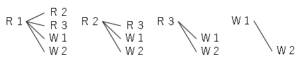
(1)
$\displaystyle \frac{3}{10}$
(2)$\displaystyle \frac{6}{10}=$
$\displaystyle \frac{3}{5}$
(3)$1-\displaystyle \frac{3}{10}=$
$\displaystyle \frac{7}{10}$
問4
1から100までのカードから1枚とるとき、以下の確率を求めよう。

(1)5の倍数の確率
(2)4または5の確率
(1)
5の倍数は5,10,15,
20,・・・,100なので20通り
よって求める確率は$\displaystyle \frac{20}{100}=$
$\displaystyle \frac{1}{5}$
(2)
4の倍数は4,8,12,16,
20,・・・,100なので25通り。
(1)より5の倍数は20通り。
これを足して・・・とやると間違いになります。
それは20,40,60,80,100をダブりで数えているからです。
つまり4×5=20の倍数を引かなくてはいけません。

よって求める確率は$\displaystyle \frac{25+20-5}{100}=$
$\displaystyle \frac{2}{5}$
問5
5本のくじの中に当たりが2つ、はずれが3つ入っている。
この中から1本引いて結果を確認して戻し、もう一度1本引く。
このとき、1本が当たり、1本がはずれである確率を求めましょう。
樹形図を書いて求めてもよいが・・・煩雑になるので
1回目にあたり(5個中2個当たり)、2回目にはずれ(5個中3個はずれ)の場合
$\displaystyle \frac{2}{5}×\displaystyle \frac{3}{5}=\displaystyle \frac{6}{25}$
2回目にあたり(5個中2個当たり)、1回目にはずれ(5個中3個はずれ)の場合
$\displaystyle \frac{3}{5}×\displaystyle \frac{2}{5}=\displaystyle \frac{6}{25}$
求める確率は
$\displaystyle \frac{6}{25}+\displaystyle \frac{6}{25}=$
$\displaystyle \frac{12}{25}$



不明点があればコメントよりどうぞ。





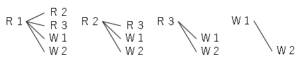











ディスカッション
コメント一覧
まだ、コメントがありません