特徴を持つ四角形の証明と面積の関係
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
平行四辺形とは
平行四辺形とは$2$組の向かい合う辺がそれぞれ平行な四角形のことを平行四辺形と言います。
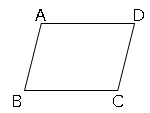
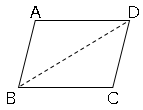
図の場合$2$組の向かい合う辺は$AB//DC$,$AD//BC$になります。
平行四辺形ならば次の性質があります。
１、平行四辺形の$2$組の向かい合う辺はそれぞれ等しい。
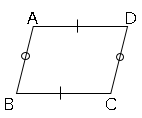
２、平行四辺形の向かいあう角はそれぞれ等しい。
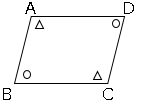
３、平行四辺形の対角線は、それぞれの中点で交わる。
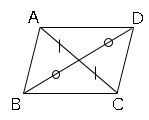
では問題です。平行四辺形$ABCD$ならば$AB=DC$,$AD=BC$を証明しましょう。
平行四辺形になる条件
５つの条件があります。
$1$.$2$組の向かいあう辺が、それぞれ平行であるとき。
$2$.$2$組の向かいあう辺はそれぞれ等しい。
$3$.$2$組の向かいあう角はそれぞれ等しい。
$4$.対角線は、それぞれの中点で交わる。
$5$.$1$組の向かいあう辺が、等しくて、平行であるとき。
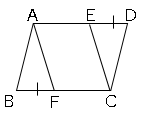
では問題です。平行四辺形$ABCD$の辺$AD$、$BC$上に、$DE$＝$BF$となる点$E$,$F$をとる。このとき$CE=AF$であることを証明しましょう。
他の四角形の特徴
以下の特徴があります。
４つの角がすべて等しい四角形を長方形といいます。
４つの辺がすべて等しい四角形をひし形といいます。
４つの辺がすべて等しく、４つの角がすべて等しい四角形を正方形といいます。
以下の性質があります。
長方形ならば、対角線の長さがそれぞれ等しい。
ひし形ならば、対角線どうしは直角に交わる。
正方形ならば、対角線の長さがそれぞれ等しく、直角に交わる。
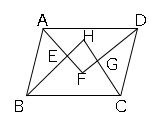
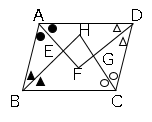
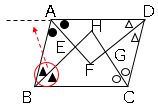
では問題です。図で、平行四辺形$ABCD$の$4$つの内角の$2$等分線の交点を$E,F,G,H$とするとき、四角形$EFGH$は長方形になることを証明しなさい。
平行線と面積の関係
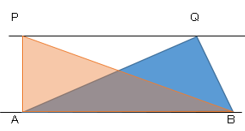
１つの直線上の２点$A$,$B$とその直線の同じ側にある点$P$,$Q$において以下が成り立つ。
１.$PQ$//$AB$ならば、△$PAB=$△$QAB$
２.△$PAB=$△$QAB$ならば、$PQ$//$AB$
簡単に説明すると、
１、$PQ$//$AB$なので、三角形の高さは等しい、また底辺$AB$も同じなので面積は同じ。
２、△$PAB=$△$QAB$なので、底辺$AB$は共通なので、高さも等しくなければいけない。よって、$PQ$//$AB$
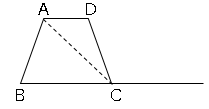
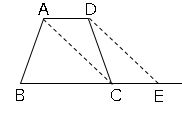
では問題です。図は$AD$//$BC$である四角形$ABCD$と同じ面積の△$ABE$を、半直線$BC$上に点$E$を取って書きなさい。
不明点があればコメントよりどうぞ。