オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
6667 Views
2019年3月16日2次関数中学3年生
問1
図のように、2つの放物線$y=ax²(a<0)$・・・➀,$y=bx²(b>0)$・・・➁がある。2点$A,B$は放物線➀上にあり、点$A$の座標は$(-2,-1)$で、線分$AB$は$x$軸に平行である。また2点$C,D$は放物線➁上にあり、線分$BC$は$y$軸に平行で、$AB=BC$である。また、点$D$は$x$座標が正で、$y$座標は$6$である。
(1)$a$の値を求めましょう。
(2)$b$の値を求めましょう。
(3)点$D$の$x$座標を求めましょう。
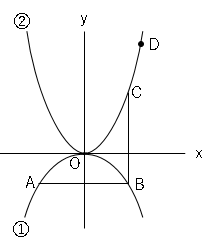
(1)

図より、点$A$の座標を代入して
$-1=4a$
$a=-\displaystyle \frac{1}{4}$
(2)
線分$AB$は$x$軸に平行なので、点$B(2,-1)$
$AB=BC$
$2+2=BC$
$BC=4$
点$B$の$y$座標は$1$なので、点$C$の$y$座標は$4-1=3$
よって$C(2,3)$
※点$B$の$x$座標と点$C$の$x$座標は等しい。
$y=bx²$に代入して
$3=4b$
$b=\displaystyle \frac{3}{4}$
(3)
点Dの座標は$y=\displaystyle \frac{3}{4}x²$上なので、
$6=\displaystyle \frac{3}{4}x²$
$8=x²$
$x=\pm2\sqrt{2}$
点$D$は$x$座標が正なので、
$x=2\sqrt{2}$
問2
図の△$ABC$の面積を求めましょう。
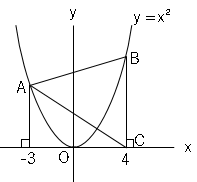

直接求められないので、工夫する。
つまり台形から三角形をひけばよい。
点$A$の$y$座標は$y=x²$に代入して、
$y=9$
点$B$の$y$座標は$y=x²$に代入して、
$y=16$
図にまとめると以下
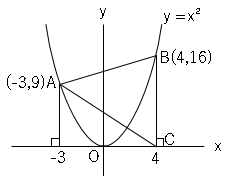
これより台形の面積は
$(9+16)×7÷2$
$=\displaystyle \frac{175}{2}$
また、三角形の面積は
$9×7÷2$
$=\displaystyle \frac{63}{2}$
求める面積は
$=\displaystyle \frac{175}{2}-\displaystyle \frac{63}{2}$
=
$56$
問3
$y=x²$と$y=x+2$が2点$A,B$で交わっているとき、△$AOB$の面積を求めましょう。
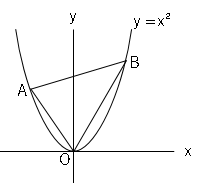

$y=x²$と$y=x+2$が2点で交わっているので、
$x²=x+2$
$x²-x-2=0$
$(x-2)(x+1)=0$
$x=-1,2$
(点$A$の座標は$y=x²$に代入して、$y=1$)
(点$B$の座標は$y=x²$に代入して、$y=4$)
また、直線$AB$と$y$軸との交点を$C$とすると、
△$AOB$の面積は△$AOC+$△$BOC$となる。
△$AOC$の面積は$2×1÷2=1$
△$BOC$の面積は$2×2÷2=2$
△$AOB$の面積は
$3$
問4
$y=\displaystyle \frac{1}{2}x²$について、$x$の値が$t$から$t+3$まで増加するときの変化の割合は$4$である。$t$の値を求めましょう。

公式に代入して、
$4=\displaystyle \frac{\displaystyle \frac{(t+3)²}{2}-\displaystyle \frac{(t)²}{2}}{t+3-t}$
$12=\displaystyle \frac{(t+3)²}{2}-\displaystyle \frac{(t)²}{2}$
$12=\displaystyle \frac{6t+9}{2}$
$24=6t+9$
$t=\displaystyle \frac{5}{2}$
問5
関数$y=ax²$について、$x$の変域が$-4≦x≦b$のとき、$y$の変域は$-48≦y≦-3$であるとき、$a,b$の値を求めなさい。

図を書くと以下のようになる。
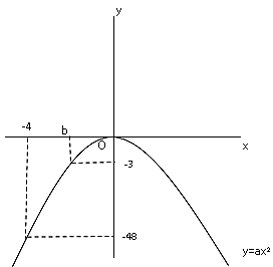
これより$a$の値を求めると
$-48=a×(-4)²$
$-48=16a$
$a=-3$
また$b$の値は$y=-3x²$に$y=-3$を代入して
$x=±1$
$+1$だと$y$の変域が$0$以上からになるので
$x=-1$
これより
$b=-1$

不明点があればコメントよりどうぞ。


















ディスカッション
コメント一覧
まだ、コメントがありません