二次関数の練習問題２

▼答えはこちらをクリック

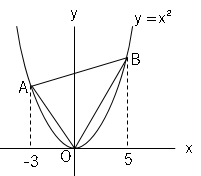
点$A,B$を出して、図に大まかな線を引く。（赤線が面積を２等分する線）

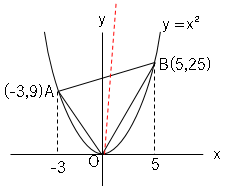
直線$AB$と赤線との交点を$C$とする。
点$C$が$AB$の中点になれば面積は２等分される。
よって
点$C(\displaystyle \frac{-3+5}{2},\displaystyle \frac{9+25}{2})$
点$C(1,17)$
これより面積を２等分する直線は$y=ax$に代入して、
$17=a$
ゆえに$y=17x$

▼答えはこちらをクリック

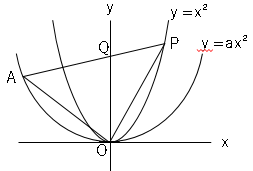
（１）
$y=ax²$のグラフに、点$A(-3,3)$があるので、
$3=9a$
$a=\displaystyle \frac{1}{3}$

（２）
△$OAQ$と△$OQP$は面積が等しいので、
底辺を$OQ$とすると、高さが同じになる。
ゆえに点$A$の$x$座標と点$P$の$x$座標が等しくなる。
よって点$P(3,9)$

更に点$Q$は中点なので、(△$OAQ$と△$OQP$は面積が等しい)
$Q(\displaystyle \frac{-3+3}{2},\displaystyle \frac{9+3}{2})$
$Q(0,6)$

よって△$AOP$の面積は
$6×3÷2+6×3÷2$
$=18$

▼答えはこちらをクリック

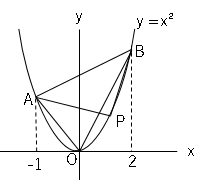
面積が同じなので、$AB$を底辺とすると高さを共通にする。
なので$AB$//$OP$、ゆえに$AB$の傾き$=OP$の傾き
点$A,B$はそれぞれ$(-1,1)$、$(2,4)$
直線の式は連立方程式より、
$\begin{eqnarray} \left\{\begin{array}{l}-a+b=1・・・➀\\2a+b=4・・・➁\end{array}\right. \end{eqnarray}$
➀$-$➁より
$-a-2a=1-4$
$a=1$

よって$OP$の傾きは$1$
直線の式は$y=x$
$y=x²$と$y=x$は２点$O,P$で交わるので、
$x²=x$
$x²-x=0$
$x(x-1)=0$
$x=0,1$
点$P$の座標は$(1,1)$