頻出の正四面体の体積

問題２２１辺が２ｃｍの正四面体の体積を求めよ。

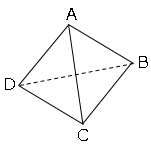
（１）

図のように点をとる。
三角形ＡＢＣにおいて点Ａから垂線をおろし、辺ＢＣとの交点をＭとする。
するとＭは中点なのでＣＭ＝１
△ＡＣＭに３平方の定理を適用してＡＭの長さを求めると
$AM²=2²-1²$
$AM=\sqrt{3}$

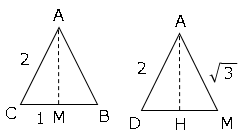
また点Ａから面ＤＣＢに垂線をおろし交点をＨとする。
次に三角形ＭＡＤを考える。
$DH=x$とすると、
$HM=\sqrt{3}-x$

よって以下の方程式が成り立つ
$AD²-DH²=AM²-HN²$
$(2)²-x²=(\sqrt{3})²-(\sqrt{3}-x)²$
$4-x²=3-3+2\sqrt{3}x-x²$
$x=\displaystyle \frac{2}{\sqrt{3}}$

これより
$AH²=(2)²-(\displaystyle \frac{2}{\sqrt{3}})²$
$AH=\sqrt{\displaystyle \frac{8}{3}}$

これより求める体積は
$2×\sqrt{3}÷2×\sqrt{\displaystyle\frac{8}{3}}÷3$
$=\displaystyle\frac{2\sqrt{2}}{3}$