正四角錐の体積

問題６

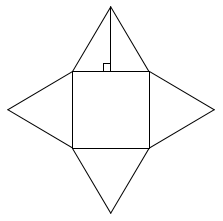
図は１辺が６ｃｍの正方形の周りに、それぞれの辺を底辺とし、高さが５ｃｍの二等辺三角形を四枚並べてみたものである。
この図形を組み合わせてできる正四角錐の体積を求めよ。

方針立体の問題は、部分的に取り出して考えるとわかりやすい。

底面と高さを求めて体積を出す。

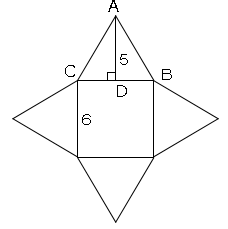
図のようにＡ,Ｂ,Ｃ,Ｄを置く。
高さは点Ａから正方形に垂線を下ろしたものであり、点をＨとする。
するとＨは正方形の中心となる。

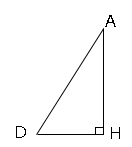
よってＤＨ＝３ｃｍとなる。
ゆえに高さは三平方の定理より
$AH²=AD²-DH²$
$AH²=5²-3²$
$AH=4$
よって図の体積は
$6×6×4÷3$
$=48$