ひもの長さと体積の関係

問題８

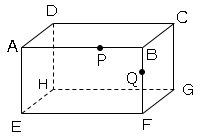
図は、ＡＢ＝６ｃｍ、ＡＤ＝２ｃｍ、ＡＥ＝４ｃｍの直方体である。
この直方体について、ＡＢ、ＢＦ上の点をそれぞれＰ，Ｑとする。
ＤＰ＋ＰＱ＋ＱＣが最小となるときの三角錐ＢＰＱＣの体積を求めなさい。

方針

ＤＰ＋ＰＱ＋ＱＣが最小とはＤ,Ｐ,Ｑ,Ｇが一直線上にあること、展開図を書いて求める。

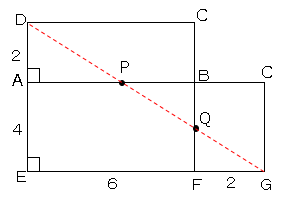
展開図を書くと上図のようになる。
それぞれの長さを相似によって求める。
△ＤＡＰ∽△ＤＥＧより
（∠Ｄ共通、∠ＤＡＰ＝∠ＤＥＧで２角が等しい）
$DA:AP=DE:EG$
$2:AP=6:8$
$AP=\displaystyle \frac{8}{3}$
これよりＢＰの長さは
$BP=AB-AP$
$BP=6-\displaystyle \frac{8}{3}$
$BP=\displaystyle \frac{10}{3}$

ＱＦの長さも相似より、
$QF:DE=FG:EG$
$QF:6=2:8$
$QF=\displaystyle \frac{3}{2}$
これよりＱＢの長さは
$QB=FB-QF$
$QB=4-\displaystyle \frac{3}{2}$
$QB=\displaystyle \frac{5}{2}$

これより求める体積は
$QB×BP÷2×BC÷3$
$=\displaystyle \frac{5}{2}×\displaystyle \frac{10}{3}÷2×2÷3$
$=\displaystyle \frac{25}{9}$