重なる円と円周の関係を推測する問題

問題１８次の図は、半径３㎝の円を《ルール》にしたがって、１番目に２個、２番目に３個、３番目に４個、…、と並べたものである。図の太線は、それぞれの図形の周囲を表す。ただし、円周率を$π$とする。


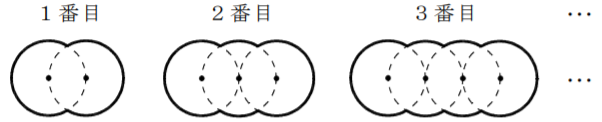
《ルール》
・それぞれの円の中心が一直線上にある。
・隣り合う円の中心の距離が半径と等しい。

(１)１番目の図形の周囲の長さを求めなさい。
(２)２番目の図形の周囲の長さは、１番目の図形の周囲の長さより何㎝長いか求めなさい。
(３)$n$番目の図形の周囲の長さを、$n$を用いた式で表しなさい。

方針

（１）
補助線をこのように引くと、

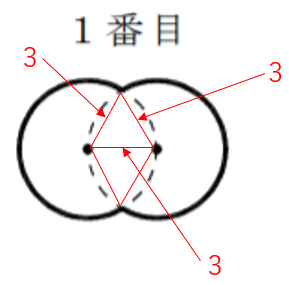
すべての辺の長さが３とわかるので、正三角形となっている。
つまり角度はすべて６０°となっている。

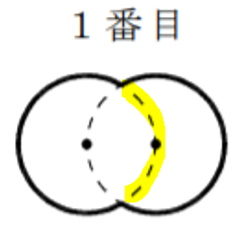
黄色の部分（円周）を求めると
$3×2×π×\displaystyle \frac{120}{360}$
$=2π$

これより求める円周は「円周－黄色の部分（円周）」を求めて２倍すればよい、
よって
$(3×2×π-2π)×2$
$=8π$

（２）

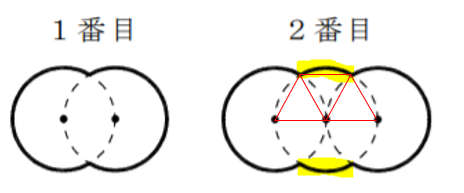
増えている部分は、黄色の箇所で図のように補助線を引くと、
中心角が６０°のおうぎ形の円周とわかる。
よって
$3×2×π×\displaystyle \frac{60}{360}$
$=π$
これが２つあるので、
$2π$

（３）
１番目の図形の円周は$8π=8π+2π×0$
２番目の図形の円周は$10π=8π+2π×1$
３番目の図形の円周は$10π=8π+2π×2$
・・・
$n$番目の図形の円周は$8π+2π×(n-1)$
$=2πn+6π$