一次関数とグラフ
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
一次関数
２つの変数$x,y$について、$y$が$x$の一次式であらわされるとき$y$は$x$の一次関数であるという。
公式：$y=ax+b$
$y=ax+b$の$a$の部分を変化の割合、$b$の部分を定数という。
また、$a=\displaystyle \frac{yの増加量}{xの増加量}$となる。
増加量についてはのちに説明します。
では問題です。
容積$50ℓ$の水槽に水が$5ℓ$入っている。この水槽に毎分$3ℓ$の割合で満水になるまで水を入れていくとき、$x$分後の水槽の水の量を$yℓ$とする。
（１）$y$を$x$の式で表せ。
（２）水を入れ始めてから$5$分後の水量を求めなさい。
（３）水槽が満水になるのは何分後ですか。
一次関数のグラフの作成
一次関数の$y=ax+b$のグラフは、$y=ax$のグラフを$y$軸の正の方向に$b$だけ平行移動させた直線である。
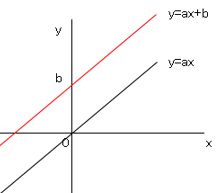
一次関数$y=ax+b$の定数部分$b$は$x=0$のときの$y$の値で、グラフが$y$軸と交わる点$(0,b)$の$y$座標になる。この$b$のことを、一次関数$y=ax+b$の切片という。
一次関数$y=ax+b$のグラフの傾き具合は$a$によって決まる。この意味で、$a$をそのグラフの傾きという。
実際にグラフを書いてみましょう。$y=-x-3$のグラフを書きましょう。
➀切片に点を打つ。
➁$y=-x-3$の任意の点(どこでも可)をグラフにとる。$x=1$のとき、$y=-4$なので、$(1,-4)$の点を打つ。
➂➀、➁の点を直線で結ぶ。
➀切片に点を打つ。このグラフの場合は$(0,3)$
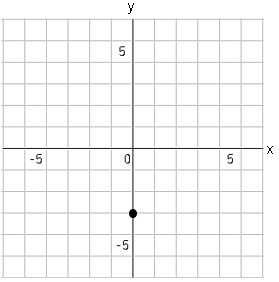
➁$y=-x-3$の任意の点(どこでも可)をグラフにとる。$x=1$のとき、$y=-4$なので、$(1,-4)$の点を打つ。
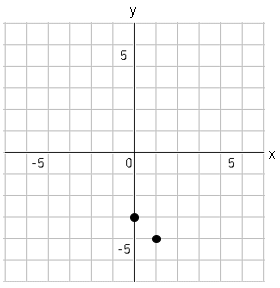
➂➀、➁の点を直線で結ぶ。
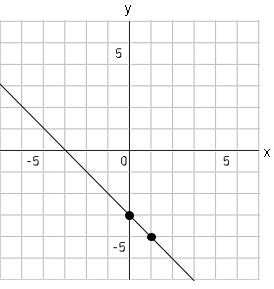
では問題です。$y=2x+2$のグラフを書きなさい。
一次関数の増加量
一次関数は$y=ax+b$で表し、$a=\displaystyle \frac{yの増加量}{xの増加量}=$$\displaystyle \frac{まで-から}{まで-から}$となる。
増加量とはどのくらい増加したかを表しています。図で理解しましょう。
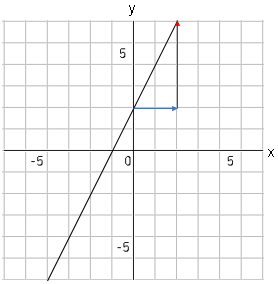
$x$が$0$から$2$まで増加するとき、$y$は$2$から$6$まで増加しています。
つまり青が$x$の増加量$(2-0=2)$、赤が$y$の増加量$(6-2=4)$になります。
公式に代入すると$a=\displaystyle \frac{4}{2}=2$となります。
関数$y=2x+4$で、$x$の値が$2$から$4$まで増加した時の$y$の増加量を求めなさい。
一次関数の傾きの関係
一次関数$y=ax+b$のグラフでは次のことが言える。
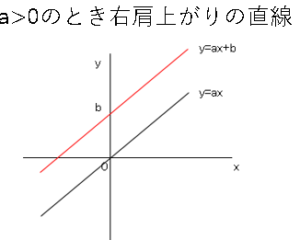
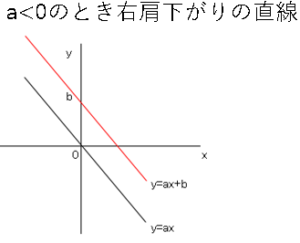
これは覚える必要はありません。具体例を書けばわかります。
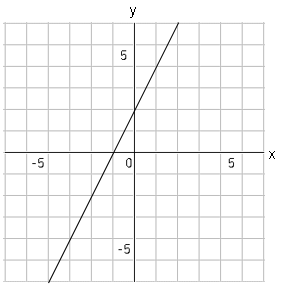
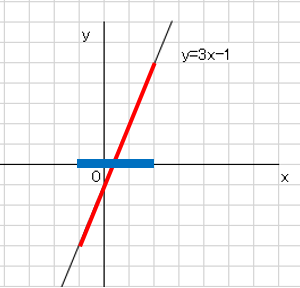
では問題です。一次関数$y=3x-1$のグラフで、$x$の変域を$-1≦x≦2$としたときの$y$の変域を求めなさい。
不明点があればコメントよりどうぞ。