度数分布
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
9264 Views
度数分布表
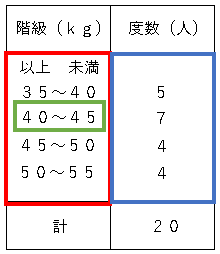
整理した１つ１つの区間を階級と言います。
各階級に入る資料の個数を、その階級の度数といい、階級に応じて、度数を上のように整理した表を度数分布表（上図）といいます。
各階級の値の幅を階級の幅と言います。この場合階級の幅は$5$。
では問題です。
次の資料は、あるクラスの男子２０人のハンドボール投げの記録である。次の問いに答えよ。
19 24 23 18 29 22 29 13 20 24 28 21 14 22 24 19 17 25 22 27 (単位：ｍ)
（１）階級の幅をもとめよう。
（２）度数分布表を埋めよう。
（３）２０ｍ以上の生徒数は全体の何％ですか。
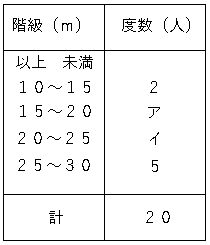
様々なグラフ
この図から２種類の図を作成してみましょう。
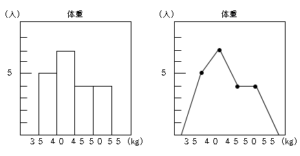
左がヒストグラム(柱状グラフ)で右が度数折れ線(度数分布多角形)といいます。度数折れ線の点の取る位置は階級の幅の真ん中にします。
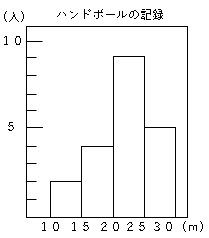
では問題です。表をヒストグラムにしてみましょう。
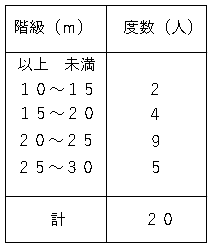
相対度数
度数分布表のそれぞれの階級について、$\displaystyle \frac{その階級の度数}{度数の合計}=相対度数$という。簡単に説明すると％を出す式で×１００をなくした式が相対度数になります。
では問題です。表の階級ごとの相対度数を求めましょう。
不明点があればコメントよりどうぞ。